CSci 39542 Syllabus    Resources    Coursework

Program 5: Tech Jobs.
CSci 39542: Introduction to Data Science
Department of Computer Science
Hunter College, City University of New York
Spring 2023

---

Classwork    Quizzes    Homework    Project   

---

---

Program Description

Program 5: Tech Jobs.   Due 10am, Wednesday, 1 March.
Learning Objective: to build intuition and strengthen competency with least squares method of minimizing functions.
Available Libraries: pandas, numpy, and core Python 3.6+.
Data Source: St. Louis Federal Reserve Bank Online Data (FRED), U Michigan BLS Monthly Job Reports Rapid Insights, November 2022
Sample Datasets:

• fred_info_2022_1yr.csv: A CSV file with the employment in Information Services for 2022.
• fred_info_2022_5yr.csv: A CSV file with the employment in Information Services for past 5 years: 2018-2022.
• fred_info_2022_all.csv: A CSV file with the employment in Information Services for all years on record (through end of 2022).

Hiring in the technical sector has been in the news recently. This program looks at the data related to information services in the United States and is inspired by Prof. Stevenson's recent analysis:

BLS Monthly Jobs Report: Rapid Insights from Betsey Stevenson

The graph above was generated in early December and includes data through November 2022. We will use data sets that include through the end of 2022 from the St. Louis Federal Reserve Economic Data (FRED). The assignment is broken into the following functions to allow for unit testing:

• parse_datetime(df, column='DATE'): This function takes two inputs:
  • df: a DataFrame containing the column column.
  • column: the name of a column. column has default value of 'DATE'.
  The function should return a DataFrame with three additional columns:
  • timestamp: contains the datetime object corresponding to the string stored in column.
  • month: return the number corresponding to the month of timestamp: 1 for January, 2 for February, ... 12 for December.
  • year: return the number corresponding to year of timestamp.
  Note this is very similar, but not identical to the parse_datetime from the DS 100: Section 9.4 or Program 4.


• compute_lin_reg(xes, yes): This function takes two inputs:
  • xes: an iterables of numeric values representing the independent variable
  • yes: an iterables of numeric values representing the dependent variable
  The function computes the slope and y-intercept of the linear regression line, using ordinary least squares (see DS 8: Chapter 15 for detailed explanation). The pseudocode for this:
  1. Compute the standard deviation of the xes and yes. Call these sd_x and sd_y.
  2. Compute the correlation, r, of the xes and yes.
  3. Compute the slope, theta_1, as theta_1 = r*sd_y/sd_x.
  4. Compute the y-intercept, theta_0, as theta_0 = average(yes) - theta_1 * average(xes)
  5. Return theta_0 and theta_1.


• predict(xes, theta_0, theta_1): This function takes three inputs:
  • xes: an iterables of numeric values representing the independent variable
  • theta_0: the y-intercept of the linear regression model
  • theta_1: the slope of the linear regression model
  The function returns the predicted values of the dependent variable, xes, under the linear regression model with y-intercept theta_0 and slope theta_1.


• mse_loss(y_actual,y_estimate):: This function takes two inputs:
  • y_actual: a Series containing numeric values.
  • y_estimate: a Series containing numeric values.
  The series are of the same length and contain numeric values only (all null and non-numeric values have been dropped). The function returns the mean square error loss function between y_actual and y_estimate (e.g. the mean of the squares of the differences).
  Note: this function was part of an earlier homework (Program 3) as well as in the textbook. It is included here to be used as a default argument for the error computation function below.


• rmse_loss(y_actual,y_estimate):: This function takes two inputs:
  • y_actual: a Series containing numeric values.
  • y_estimate: a Series containing numeric values.
  The series are of the same length and contain numeric values only (all null and non-numeric values have been dropped). The function returns the square root of the mean square error loss function between y_actual and y_estimate (e.g. the square root of the mean of the squares of the differences).


• compute_error(y_actual,y_estimate,loss_fnc=mse_loss): This function takes three inputs:
  • y_actual: a Series containing numeric values.
  • y_estimate: a Series containing numeric values.
  • loss_fnc: function that takes two numeric series as input parameters and returns a numeric value. It has a default value of mse_loss.
  The series are of the same length and contain numeric values only (all null and non-numeric values have been dropped). The result of computing the loss_fnc on the inputs y_actual and y_estimate is returned.


• compute_ytd(df): This function takes one input:
  • df: a DataFrame containing columns month, year and USINFO.
  The function returns a Series with the number of jobs since the beginning of the year for that entry. For example, for the January 2022 row, the number would be 0 since January is the beginning of the year. For July 2022, the number be the difference between USINFO for July and USINFO for January.


• compute_year_over_year(df): This function takes one input:
  • df: a DataFrame containing columns month, year and USINFO.
  Computes and returns a Series with the percent change from the previous year for USINFO. You can assume that the DataFrame is ordered by date, with earlier dates coming first in the DataFrame.
  Note: you may find the pd.pct_change function useful for computing the change from the previous year.

Let's start with the 2022 numbers:

df_1yr = pd.read_csv('program05/fred_info_2022_1yr.csv')
df_1yr = parse_datetime(df_1yr)
print(df_1yr)

would print:

          DATE  USINFO  timestamp  month  year
0   2021-12-01    2913 2021-12-01     12  2021
1   2022-01-01    2918 2022-01-01      1  2022
2   2022-02-01    2918 2022-02-01      2  2022
3   2022-03-01    2936 2022-03-01      3  2022
4   2022-04-01    2957 2022-04-01      4  2022
5   2022-05-01    2983 2022-05-01      5  2022
6   2022-06-01    3009 2022-06-01      6  2022
7   2022-07-01    3025 2022-07-01      7  2022
8   2022-08-01    3032 2022-08-01      8  2022
9   2022-09-01    3040 2022-09-01      9  2022
10  2022-10-01    3044 2022-10-01     10  2022
11  2022-11-01    3066 2022-11-01     11  2022
12  2022-12-01    3061 2022-12-01     12  2022

Note that the columns DATE and timestamp are printed the same, but if we check the types, they are stored as strings and datetime, respectively:

print(f'df_1yr has elements of:\n {df_1yr.dtypes}')

which prints:

df_1yr has elements of:
DATE                 object
USINFO                int64
timestamp    datetime64[ns]
month                 int64
year                  int64 

Exploring the 2022 job numbers:

import seaborn as sns
import matplotlib.pyplot as plt
sns.lineplot(data = df_1yr, x = 'month', y='USINFO')
plt.ylabel('Number of Jobs')
plt.xticks(range(1,13),\
    ['Jan','Feb','Mar','Apr','May','Jun','Jul','Aug','Sep','Oct','Nov','Dec'])
plt.title('Information Services Employment, 2022')
plt.show()

The additional data from December shows a drop-off:

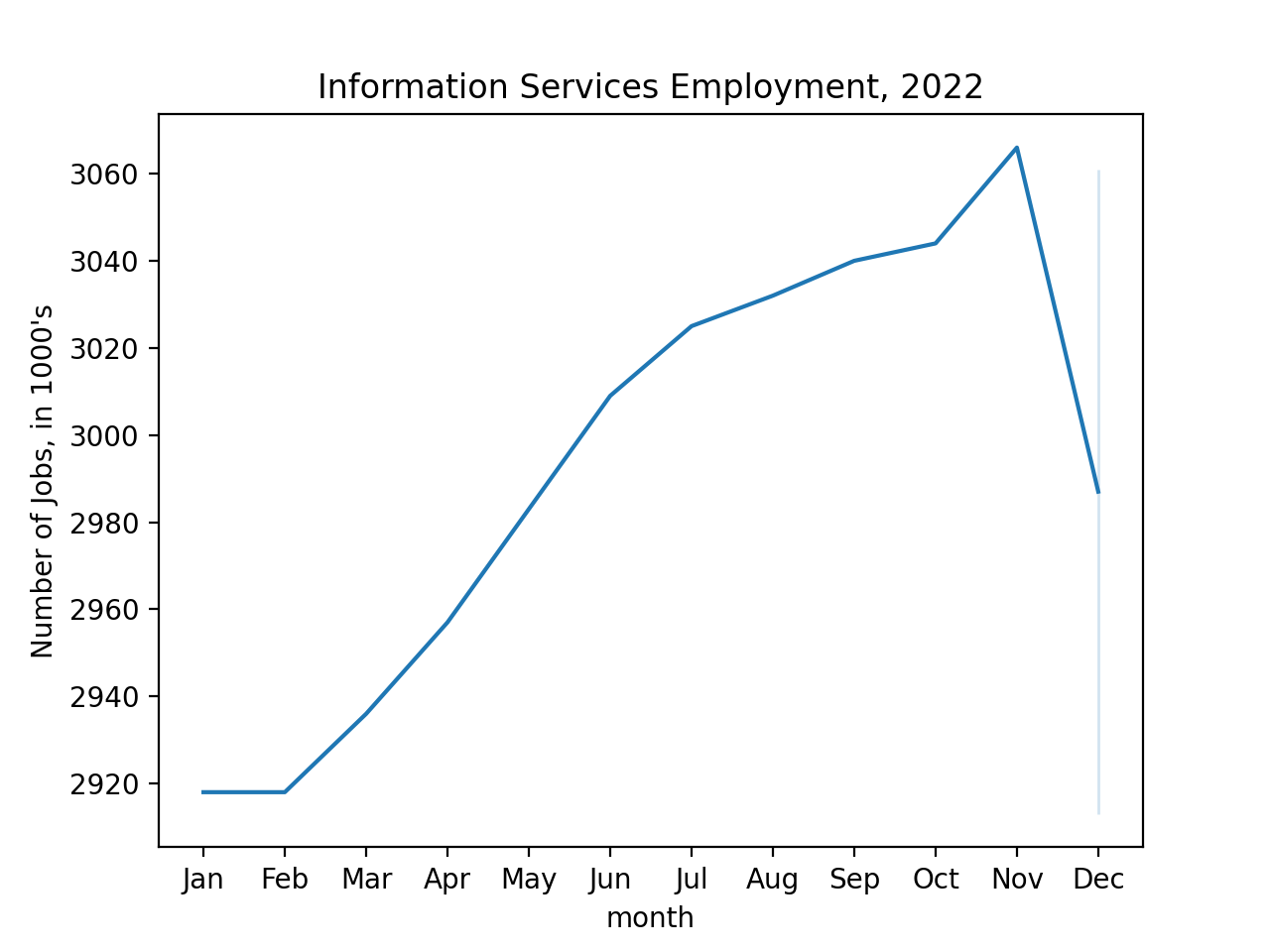
Let's fit a regression line to the 2022 numbers:

theta_0, theta_1 = compute_lin_reg(df_1yr['month'],df_1yr['USINFO'])
xes = np.array([0,12])
yes = theta_1*xes + theta_0
sns.lineplot(data = df_1yr, x = 'month', y='USINFO')
plt.ylabel("Number of Jobs, in 1000's")
plt.xticks(range(1,13),\
    ['Jan','Feb','Mar','Apr','May','Jun','Jul','Aug','Sep','Oct','Nov','Dec'])
plt.plot(xes,yes)
plt.title(f'Regression line with m = {theta_1:.2f} and y-intercept = {theta_0:.2f}')
plt.show()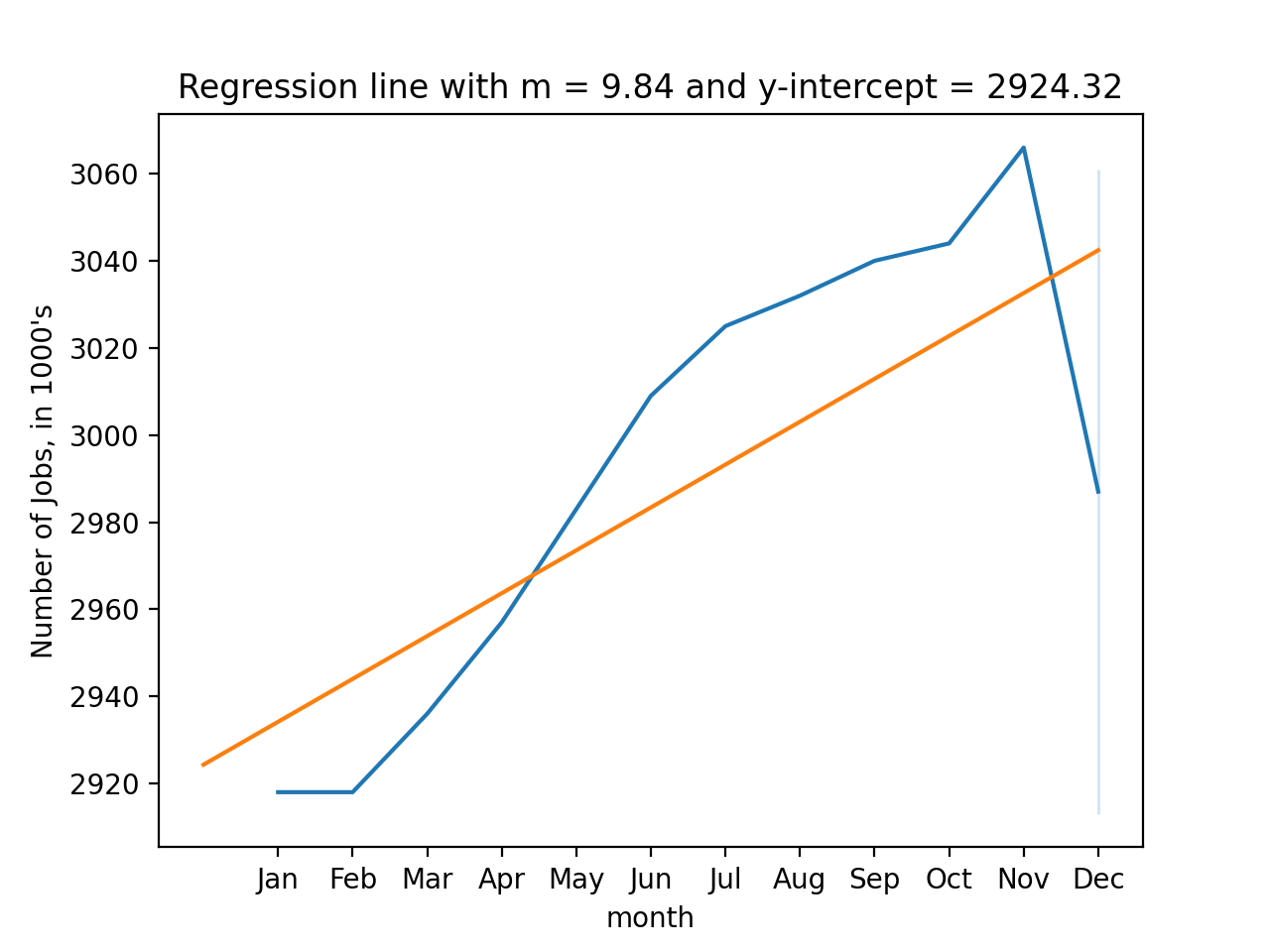    

would give the plot:

We can also use the theta values to estimate future values. For example, since if we were to extend our count of months into 2023, we can compute the predicted number of jobs:

months_2023 = np.array([13,14,15,16,17])
  print(predict(months_2023,theta_0,theta_1)*1000)

which would print:

[3052279.02790279 3062122.41224122 3071965.79657966 3081809.18091809
  3091652.56525653]

showing 3,052,280 jobs in January and gaining an additional 40,000 jobs by May 2023.

We can repeat our calculations using data from the last 5 years, but since we have more than 1 year, we can't use the month as our x-axis. Instead, we can use the index:

df_5yr = pd.read_csv('program05/fred_info_2022_5yr.csv')
df_5yr = parse_datetime(df_5yr)
print(df_5yr[:30])
print(df_5yr.index.to_series())

which will print:

          DATE  USINFO  timestamp  month  year
0   2012-12-01    2675 2012-12-01     12  2012
1   2013-01-01    2661 2013-01-01      1  2013
2   2013-02-01    2699 2013-02-01      2  2013
3   2013-03-01    2699 2013-03-01      3  2013
4   2013-04-01    2696 2013-04-01      4  2013
5   2013-05-01    2711 2013-05-01      5  2013
6   2013-06-01    2707 2013-06-01      6  2013
7   2013-07-01    2720 2013-07-01      7  2013
8   2013-08-01    2690 2013-08-01      8  2013
9   2013-09-01    2707 2013-09-01      9  2013
10  2013-10-01    2719 2013-10-01     10  2013
11  2013-11-01    2724 2013-11-01     11  2013
12  2013-12-01    2726 2013-12-01     12  2013
13  2014-01-01    2721 2014-01-01      1  2014
14  2014-02-01    2719 2014-02-01      2  2014
15  2014-03-01    2725 2014-03-01      3  2014
16  2014-04-01    2722 2014-04-01      4  2014
17  2014-05-01    2719 2014-05-01      5  2014
18  2014-06-01    2725 2014-06-01      6  2014
19  2014-07-01    2724 2014-07-01      7  2014
20  2014-08-01    2731 2014-08-01      8  2014
21  2014-09-01    2732 2014-09-01      9  2014
22  2014-10-01    2726 2014-10-01     10  2014
23  2014-11-01    2735 2014-11-01     11  2014
24  2014-12-01    2735 2014-12-01     12  2014
25  2015-01-01    2738 2015-01-01      1  2015
26  2015-02-01    2742 2015-02-01      2  2015
27  2015-03-01    2737 2015-03-01      3  2015
28  2015-04-01    2741 2015-04-01      4  2015
29  2015-05-01    2749 2015-05-01      5  2015
0        0
1        1
2        2
3        3
4        4
      ... 
116    116
117    117
118    118
119    119
120    120
Length: 121, dtype: int64

Using the index for the x values:

theta_0, theta_1 = compute_lin_reg(df_5yr.index.to_series(),df_5yr['USINFO'])
print(theta_0, theta_1)
df_5yr['predicted'] = theta_1*df_5yr.index.to_series() + theta_0
sns.lineplot(data = df_5yr, x = 'timestamp', y='USINFO')
sns.lineplot(data = df_5yr, x = 'timestamp', y='predicted')
plt.ylabel("Number of Jobs, in 1000's")
plt.xlabel("2018-2022")
plt.title(f'Regression line with m = {theta_1:.2f} and y-intercept = {theta_0:.2f}')
plt.show()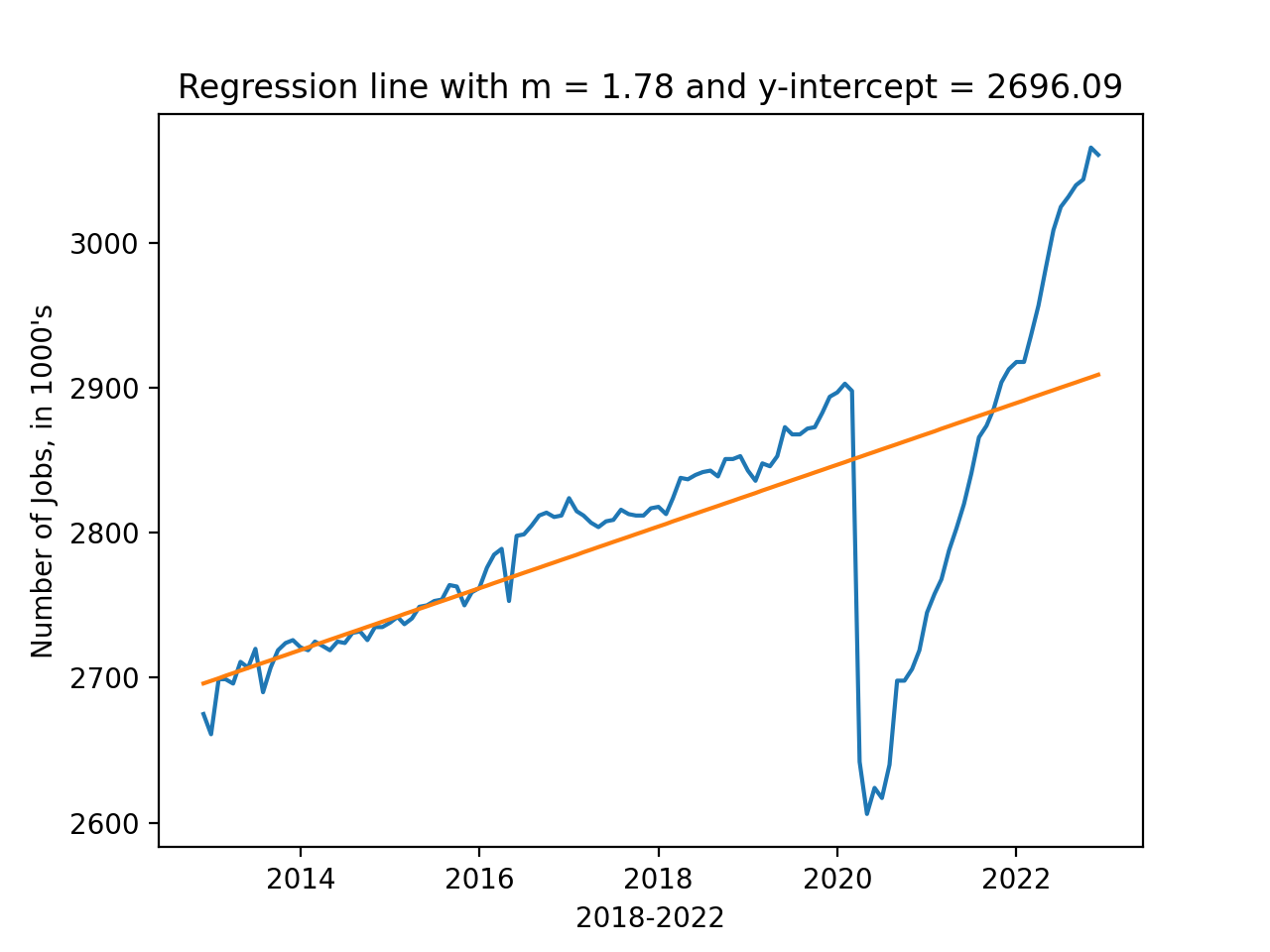

would give the plot:

Using seaborn's functionality with time series data, we can look at year-to-date growth of jobs for the last ten years, highlighting 2022 in blue:

df_all = pd.read_csv('program05/fred_info_2022_all.csv')
df_all = parse_datetime(df_all)
print(df_all)
df_all['YTD'] = compute_ytd(df_all)

sns.lineplot(data=df_all[-120:], x = 'month', y='YTD', units='year',\
            estimator=None, color=".7", linewidth=1)
sns.lineplot(data=df_all[-12:], x = 'month', y='YTD', linewidth=2)
plt.ylabel("Year To Date, in 1000's")
plt.xticks(range(1,13),\
    ['Jan','Feb','Mar','Apr','May','Jun','Jul','Aug','Sep','Oct','Nov','Dec'])
plt.title('Year To Date, 2013-2022')
plt.show()   

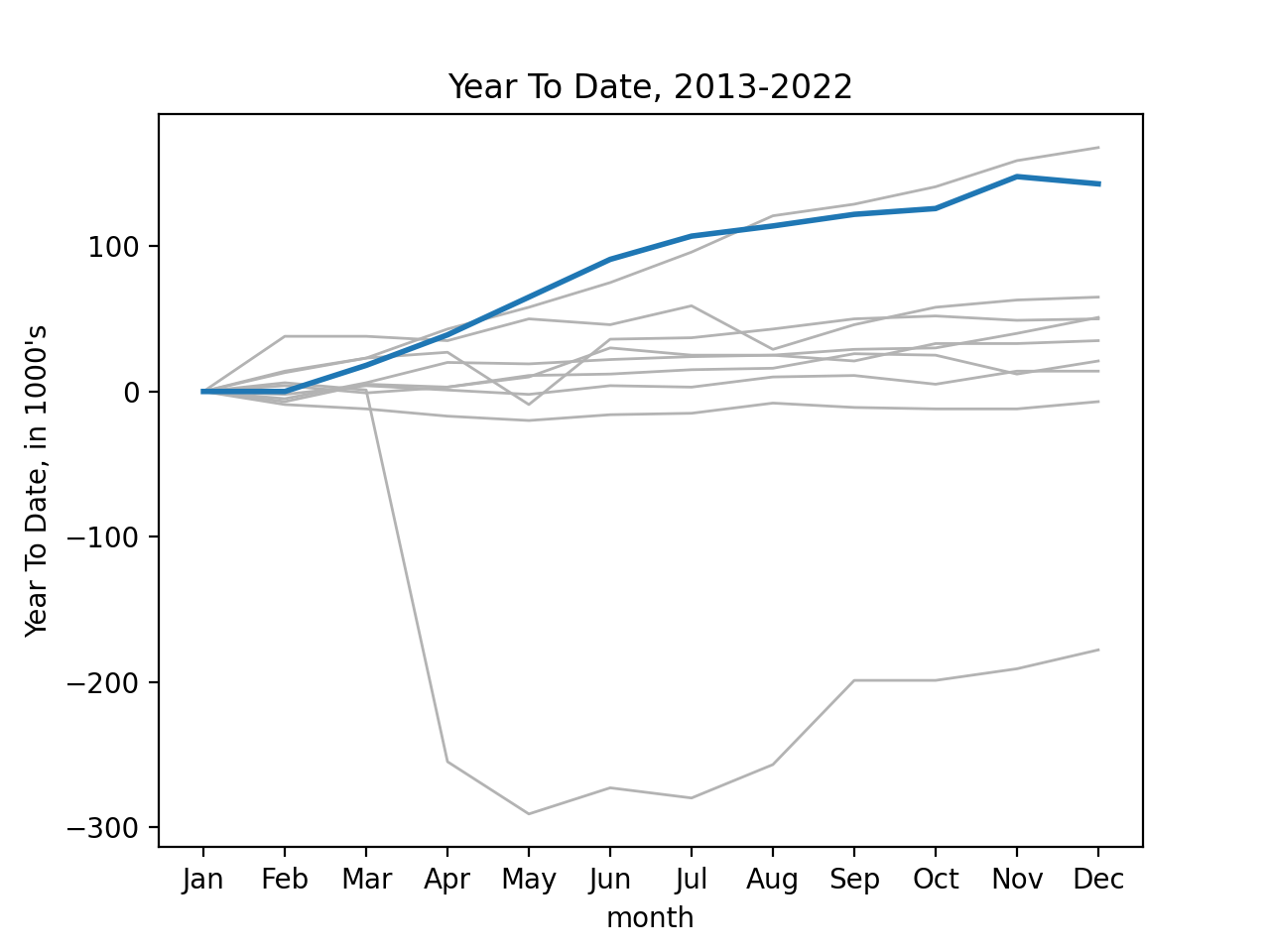
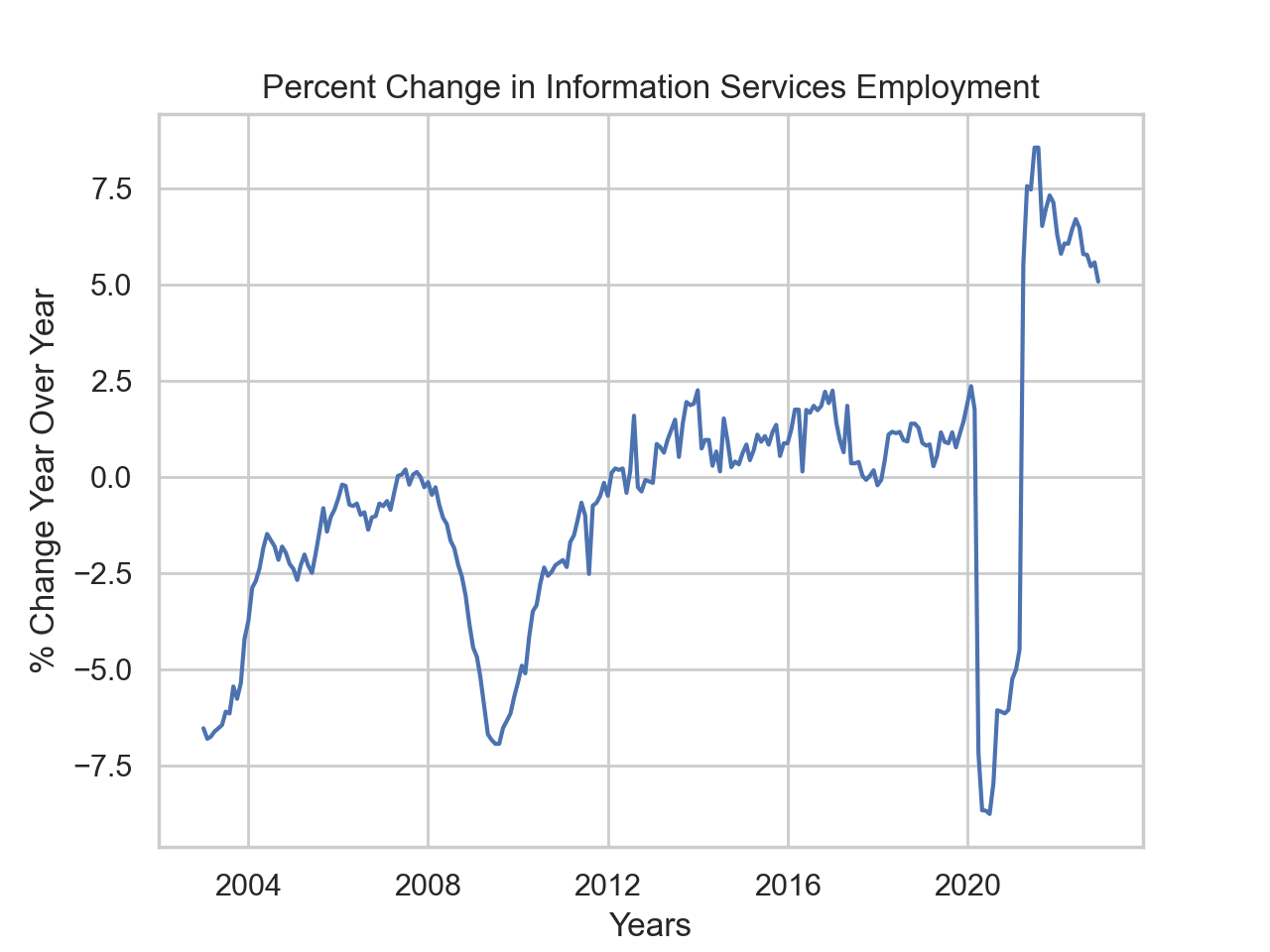
Looking at the change, measured against previous year:

df_all['YTD'] = compute_ytd(df_all)
df_all['year_over_year'] = compute_year_over_year(df_all)
sns.set_theme(style="whitegrid")
sns.lineplot(data=df_all[-240:],x='timestamp',y='year_over_year')
plt.ylabel('% Change Year Over Year')
plt.xlabel('Years')
plt.title('Percent Change in Information Services Employment')
plt.show()

we see slowing, but continued growth:

Notes and Hints:

• You should submit a .py file with only the standard comments at the top, the specified functions, and any helper functions you have written. The grading scripts will then import the file for testing. If your file includes code outside of functions, either comment the code out before submitting or use a main function that is conditionally executed (see Think CS: Section 6.8 for details).
• Include only the libraries you need (such as pandas) for your functions and none of the ones for plotting (such as matplotlib.pyplot and seaborn) since the functions submitted are computing and not plotting. Only the libraries listed in Available Libraries are loaded by the autograder.
• See Lecture 3 or DS 100: Section 9.4 for working with dates and times.