CSci 39542 Syllabus    Resources    Coursework


Program 4: Taxi Classifiers
CSci 39542: Introduction to Data Science
Department of Computer Science
Hunter College, City University of New York
Spring 2022

Classwork    Quizzes    Homework    Project   

Program Description


Program 4: Taxi Classifiers.   Due noon, Friday, 27 October.
Learning Objective: to train and validate models, given quantitative and qualitative data, as well as assessing model quality.
Available Libraries: pandas, datetime, pickle, pytest, sklearn.ensemble, sklearn.model_selection, sklearn.metrics, sklearn.svm, and core Python 3.6+. (Note if you use our annonations, you should also import Union.)
Data Sources: 2021 Yellow Taxi Trip Data and NYC Taxi Zones from OpenData NYC.
Sample Datasets: taxi_new_years_day_2021.csv, taxi_4July2021.csv, taxi_jfk_june2021.csv, and taxi_zones.csv.
This program is tailored to the NYC OpenData Yellow Taxi Trip Data and follows standard strategy for data cleaning and model building:

  1. Read in datasets, merging and cleaning as needed.
  2. Impute missing values (we will use median for the ordinal values and "most popular" for nominal values).
  3. Use categorical encoding for qualitative values.
  4. Split our dataset into training and testing sets.
  5. Fit a model, or multiple models, to the training dataset.
  6. Validate the models using the testing dataset.
  7. Develop test suites, using pytest, to ensure that correctness of your code.
To identify which trips are most likely to cross between boroughs, this program will focus on building several classifiers on both the categorical and numerical features of our dataset.

image of yellow taxi

NYC OpenData Yellow Taxi Trip Data

This program uses two datasets from NYC Open Data:

See Program 1 for directions on how to download datasets from NYC Open Data. The sample datasets are filtered, before downloading, by pickup time tpep_pickup_datetime and pickup location PULocationID. Create a practice dataset from your birthday or favorite day in 2021 to use to test your code.

Preparing Data

Once you have downloaded some test data sets to your device, the next thing to do is format the data to be usable for analysis. We will need to do some cleaning, as well as imputing missing values and encoding categorical values. Once we have the cleaned the data, we can split it into training and testing data sets. Add the following functions to your Python program:



For example, let's start by setting up a DataFrame, with the file, taxi_4July2021.csv, add in the tip and time features, and imputing missing values for passenger_count: 

df = import_data('taxi_4July2021.csv')
df = add_tip_time_features(df)
print('First lines of DataFrame with tip/time features:')
print(df.head())
which prints: 
   VendorID    tpep_pickup_datetime   tpep_dropoff_datetime  passenger_count  trip_distance  ...  tolls_amount  total_amount  percent_tip  duration  dayofweek
0       1.0  07/04/2021 12:00:00 AM  07/04/2021 12:16:03 AM              2.0           3.50  ...           0.0         20.75    19.942197     963.0          6
1       NaN  07/04/2021 12:00:00 AM  07/04/2021 12:08:00 AM              NaN           1.49  ...           0.0         16.30    13.986014     480.0          6
2       NaN  07/04/2021 12:00:00 AM  07/04/2021 12:09:00 AM              NaN           1.66  ...           0.0         17.01    15.793057     540.0          6
3       NaN  07/04/2021 12:00:00 AM  07/04/2021 12:18:00 AM              NaN           3.75  ...           0.0         24.65    21.428571    1080.0          6
4       NaN  07/04/2021 12:00:00 AM  07/04/2021 12:15:00 AM              NaN           5.07  ...           0.0         32.50     0.000000     900.0          6

[5 rows x 14 columns]
Next, let's use our new functions to impute passenger counts and add in boroughs for the pick up and drop off locations: 
df = impute_numeric_cols(df,['passenger_count'])
df = add_boro(df,'taxi_zones.csv')
print('\nThe locations and new columns:')
print(f"{df[['passenger_count','PULocationID','PU_borough','DOLocationID','DO_borough']]}")

which prints out the new columns: 

The locations and new columns:
       passenger_count  PULocationID PU_borough  DOLocationID DO_borough
0                  2.0           170  Manhattan           238  Manhattan
1                  1.0           107  Manhattan           246  Manhattan
2                  1.0           113  Manhattan           186  Manhattan
3                  1.0           137  Manhattan           256   Brooklyn
4                  1.0           151  Manhattan            68  Manhattan
...                ...           ...        ...           ...        ...
60286              1.0           186  Manhattan            68  Manhattan
60287              1.0           234  Manhattan           249  Manhattan
60288              1.0            90  Manhattan           230  Manhattan
60289              1.0            79  Manhattan           144  Manhattan
60290              1.0           186  Manhattan           229  Manhattan

We can add the indicators for if a toll was paid and if the trip started and ended in different boroughs: 

df = add_flags(df)
print(df[['trip_distance','PU_borough','DO_borough','paid_toll','cross_boro']])
prints: 
       trip_distance PU_borough DO_borough  paid_toll  cross_boro
0               3.50  Manhattan  Manhattan          1           0
1               1.49  Manhattan  Manhattan          1           0
2               1.66  Manhattan  Manhattan          1           0
3               3.75  Manhattan   Brooklyn          1           1
4               5.07  Manhattan  Manhattan          1           0
...              ...        ...        ...        ...         ...
60282           0.60  Manhattan  Manhattan          1           0
60283           1.43  Manhattan  Manhattan          1           0
60284           1.57  Manhattan  Manhattan          1           0
60285           0.89  Manhattan  Manhattan          1           0
60286           2.09  Manhattan  Manhattan          1           0

Let's explore the data some: 

import matplotlib.pyplot as plt
import seaborn as sns
sns.set_theme(color_codes=True)

sns.boxplot(data=df, x="trip_distance")
plt.title('Plot of trip_distance')
plt.tight_layout()  #for nicer margins
plt.show()

sns.boxplot(data=df, x="duration")
plt.title('Plot of duration')
plt.tight_layout()  #for nicer margins
plt.show()

The resulting plots are:

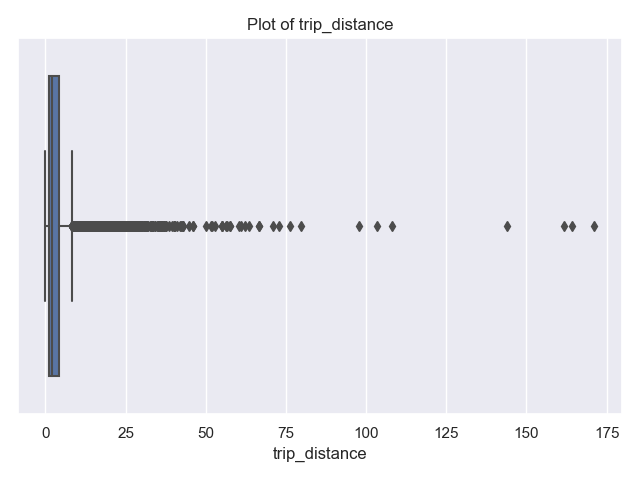
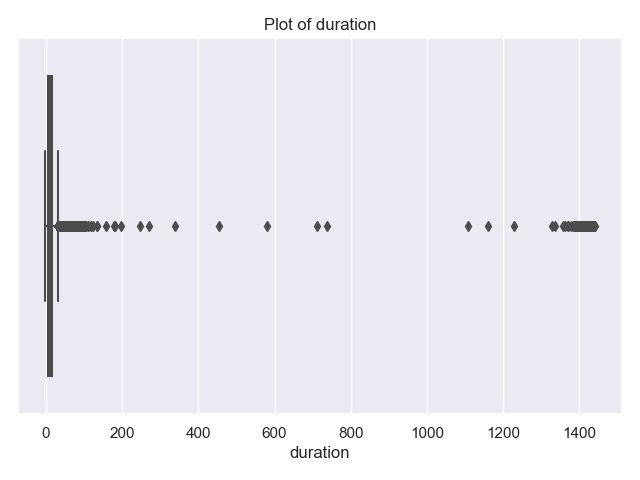
and show that most trips are short in distance and time. There's a some long trips and very long durations. The latter are likely measurement errors (e.g. mistakenly not ending the trip on the trip recorder), since it's unlikely that there are many trips of 240 minutes (4 hours) or more.

Let's look at the trips of over 4 hours and also those of more than 100 miles:

print(df[['trip_distance','duration']])
print('Trips that are longer than 4 hours:')
print(df[ df['duration'] >60*4][["tpep_pickup_datetime","tpep_dropoff_datetime","trip_distance","duration"]])
print(f"Max trip for long trips is: {df[ df['duration'] >60*4]['trip_distance'].max()}")
Trips that are longer than 4 hours:
    tpep_pickup_datetime   tpep_dropoff_datetime  trip_distance     duration
90     07/04/2021 12:01:43 AM  07/04/2021 11:27:14 PM           2.40  1405.516667
524    07/04/2021 12:10:51 AM  07/04/2021 11:42:47 PM           3.87  1411.933333
1240   07/04/2021 12:26:42 AM  07/04/2021 10:34:47 PM           1.85  1328.083333
1560   07/04/2021 12:34:18 AM  07/05/2021 12:32:39 AM           1.99  1438.350000
2341   07/04/2021 12:52:52 AM  07/04/2021 08:27:48 AM          19.31   454.933333
...                       ...                     ...            ...          ...
58554  07/04/2021 11:18:59 PM  07/05/2021 11:15:07 PM           3.54  1436.133333
59505  07/04/2021 11:41:01 PM  07/05/2021 11:26:59 PM           3.18  1425.966667
59690  07/04/2021 11:45:17 PM  07/05/2021 10:34:01 PM          17.17  1368.733333
60154  07/04/2021 11:56:51 PM  07/05/2021 11:32:48 PM           1.17  1415.950000
60172  07/04/2021 11:57:05 PM  07/05/2021 10:34:14 PM          19.60  1357.150000

[157 rows x 4 columns]
Max trip for long trips is: 19.86

The farthest traveled of the 157 trips that took more than 4 hours is just under 19.86. This seems much more likely an error in the recording device than actual trips. Let's look at the long trips:

print('Trips that are longer than 100 miles:')
print(df[ df['trip_distance'] >100][["tpep_pickup_datetime","tpep_dropoff_datetime","trip_distance","duration"]])
tpep_pickup_datetime   tpep_dropoff_datetime  trip_distance   duration
14080  07/04/2021 10:43:03 AM  07/04/2021 10:58:24 AM          108.2  15.350000
17162  07/04/2021 11:49:17 AM  07/04/2021 12:06:09 PM          103.3  16.866667
27029  07/04/2021 02:28:57 PM  07/04/2021 02:48:52 PM          171.1  19.916667
33158  07/04/2021 04:00:19 PM  07/04/2021 04:21:38 PM          161.6  21.316667
35624  07/04/2021 04:36:21 PM  07/04/2021 04:51:59 PM          144.0  15.633333
40783  07/04/2021 05:53:22 PM  07/04/2021 06:24:52 PM          164.2  31.500000

To focus on trips that stay within the city, let's limit our data to trips that are less than 50 miles in distance, as well as less than 4 hours in duration. And, explore the data by making scatter plots of some of the features: 

df = df[ df['duration'] < 60*4]
df = df[df['trip_distance'] < 50]
  
sns.lmplot(x="trip_distance", y="duration", data=df)
tot_r = df['trip_distance'].corr(df['duration'])
plt.title(f'Taxi Trips from 4 July 2021 with r = {tot_r:.2f}')
plt.tight_layout()  #for nicer margins
plt.show()
sns.lmplot(x="trip_distance", y="paid_toll", data=df,fit_reg=False,y_jitter=0.1,
            scatter_kws={'alpha': 0.3})
dist_r = df['trip_distance'].corr(df['paid_toll'])
plt.title(f'Taxi Trips from 4 July 2021 with r = {dist_r:.2f}')
plt.tight_layout()  #for nicer margins
plt.show()
sns.lmplot(x="trip_distance", y="cross_boro", data=df,fit_reg=False,y_jitter=0.1,
            scatter_kws={'alpha': 0.3})
dist_r = df['trip_distance'].corr(df['cross_boro'])
plt.title(f'Taxi Trips from 4 July 2021 with r = {dist_r:.2f}')
plt.tight_layout()  #for nicer margins
plt.show()

As discussed in Lecture 8 and Chapter 24, we added jitter to the y-values to better visualize the data since so much has similar values:

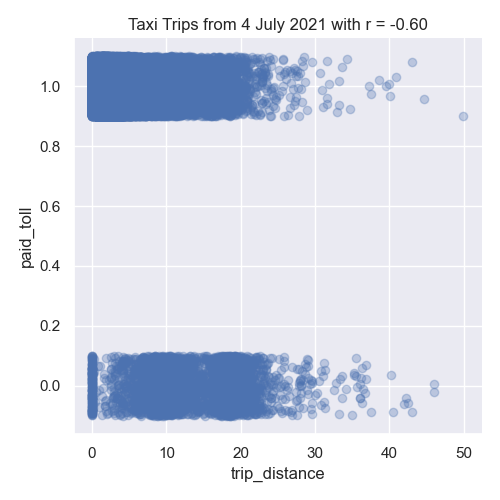
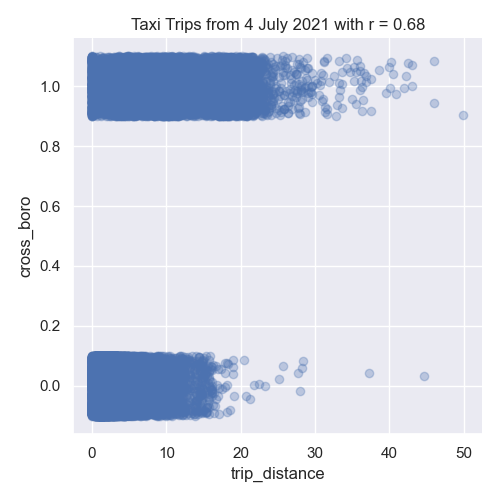
In our left image, the distance traveled and the duration of the trip are strongly correlated. The middle image show negative correlation between trip distance and paying tolls. While the right images shows the trip distance positively correlated with trips that start and end in different boroughs.

Next, let's encode the categorical columns for pick up and drop off boroughs so we can use them as inputs for our model. 

df_pu = encode_categorical_col(df['PU_borough'],'PU_')
print(df_pu.head())
df_do = encode_categorical_col(df['DO_borough'],'DO_')
print(df_do.head())

The first few lines of the resulting DataFrames: 

   PU_Bronx  PU_Brooklyn  PU_EWR  PU_Manhattan  PU_Queens
0         0            0       0             1          0
1         0            0       0             1          0
2         0            0       0             1          0
3         0            0       0             1          0
4         0            0       0             1          0
    DO_Bronx  DO_Brooklyn  DO_EWR  DO_Manhattan  DO_Queens
0         0            0       0             1          0
1         0            0       0             1          0
2         0            0       0             1          0
3         0            1       0             0          0
4         0            0       0             1          0

Let's combine all the DataFrames into one (using concat along column axis): 

df_all = pd.concat( [df,df_pu,df_do], axis=1)
  print(f'The combined DataFrame has columns: {df_all.columns}')

The combined DataFrame has the columns: 

The combined DataFrame has columns: 
Index(['VendorID', 'tpep_pickup_datetime', 'tpep_dropoff_datetime',
       'passenger_count', 'trip_distance', 'PULocationID', 'DOLocationID',
       'fare_amount', 'tip_amount', 'tolls_amount', 'total_amount',
       'percent_tip', 'duration', 'dayofweek', 'PU_borough', 'DO_borough',
       'paid_toll', 'cross_boro', 'PU_Bronx', 'PU_Brooklyn', 'PU_EWR',
       'PU_Manhattan', 'PU_Queens', 'DO_Bronx', 'DO_Brooklyn', 'DO_EWR',
       'DO_Manhattan', 'DO_Queens'],
     dtype='object')
For the taxi data, there is a special zone for trips to Newark Airport, and as such we have a drop off borough location of 'DO_EWR'. We'll focus on the numeric columns, split our data into training and testing data sets: 
x_col_names = ['passenger_count', 'trip_distance', 'RatecodeID', 'PULocationID',
            'DOLocationID', 'payment_type', 'fare_amount', 'extra', 'mta_tax',
            'tip_amount', 'tolls_amount', 'improvement_surcharge', 'total_amount',
            'congestion_surcharge', 'percent_tip', 'duration', 'dayofweek',
            'paid_toll', 'PU_Bronx', 'PU_Brooklyn', 'PU_Manhattan', 'PU_Queens',
            'DO_Bronx', 'DO_Brooklyn', 'DO_EWR', 'DO_Manhattan', 'DO_Queens']
y_col_name = 'cross_boro'
x_train, x_test, y_train, y_test = split_test_train(df_all, x_col_names, y_col_name)


Building Classifers

In Lectures 8 & 9, we introduced models for classifying data. We will use three of those classifiers here: logistic regression, support vector machine classifier (SVC), and random forests. All are implemented in scikit-learn and we will

We'll use these functions to build a list of models (as serialized objects) for later use. We'll try first just a single independent variable, trip_distance, and build a classifiers to predict when trips start in one borough and end in another (when cross_boro is 1). Since some classifiers expect data to be in standard units (introduced in lecture and Program 2), we first put the training sets in standard units and transform the testing sets to be in the same units: 

from sklearn.preprocessing import StandardScaler
x_cols = ['trip_distance','dayofweek','paid_toll', 'PU_Bronx', 'PU_Brooklyn','PU_Manhattan', 'PU_Queens']
x_scaler = StandardScaler()
x_tr_std = x_scaler.fit_transform(x_train[x_cols])
x_te_std = x_scaler.transform(x_test[x_cols])

print(f'The means for the x_scaler is {x_scaler.mean_} and x_tr_std is {(np.mean(x_tr_std))}')

The means for our data are:

The means for the x_scaler is [3.76803337 6.         0.93331411 0.00672183 0.01936686 0.8738381
      0.08807152] and x_tr_std is 3.485845347030431e-17

For each type of classifier, we will set up a model for the different parameters available:

pkl_models = []
mod_names = []
for p in [None,'l1','l2']:
  print(f'Fitting a logistic model with {p} regularization.')
  mod_names.append(f'logistic regression with {p} regularization')
  pkl_models.append(fit_logistic_regression(x_tr,y_tr,penalty=p))
for n_trees in [10,100,1000]:
  print(f'Fitting a random forest model with {p} number of trees.')
  mod_names.append(f'random forest with {p} number of trees')
  pkl_models.append(fit_random_forest(x_tr,y_tr,num_trees=n_trees)) 
for kernel in ['linear', 'poly', 'rbf','sigmoid']:
  print(f'Fitting a SVC with {p} kernel.')
  mod_names.append(f'SVC with {p} kernel')
  pkl_models.append(fit_svc(x_tr,y_tr,kernel=kernel),max_iter=50000)

Note that we increased the number of iterates for the SVM classifier, since the default of 1000 gave convergence warnings, but even at 50,000, the poly kernel gave convergence warnings:

Fitting a logistic model with None regularization.
Fitting a logistic model with l1 regularization.
Fitting a logistic model with l2 regularization.
Fitting a random forest model with 10 number of trees.
Fitting a random forest model with 100 number of trees.
Fitting a random forest model with 1000 number of trees.
Fitting a SVC with linear kernel.
Fitting a SVC with poly kernel.
/Users/stjohn/opt/anaconda3/lib/python3.8/site-packages/sklearn/svm/_base.py:299: ConvergenceWarning: Solver terminated early (max_iter=50000).  Consider pre-processing your data with StandardScaler or MinMaxScaler.
  warnings.warn(
Fitting a SVC with rbf kernel.
Fitting a SVC with sigmoid kernel.

Evaluating Our Classifiers

We have build a list of multiple classifiers and now will evaluate how well each works on the training data as well as the data we saved for testing.

Let's run the logistic models we build above: 

print(f'For independent variables:  {x_cols}:')
for mod,name in zip(mod_list[:3],name_list[:3]):
    print(f'For model {name}:')
    mse_tr, r2_tr = predict_using_trained_model(mod,x_tr_std,y_train)
    print(f'\ttraining data: mean squared error = {mse_tr:8.8} and r2 = {r2_tr:4.4}.')
    mse_val, r2_val = predict_using_trained_model(mod,x_te_std,y_test)
    print(f'\ttesting data: mean squared error = {mse_val:8.8} and r2 = {r2_val:4.4}.')
which prints: 
For independent variables:  ['trip_distance', 'dayofweek', 'paid_toll', 'PU_Bronx', 'PU_Brooklyn', 'PU_Manhattan', 'PU_Queens']:
For model logistic regression with None regularization:
        training data: mean squared error = 0.070102269 and r2 = 0.5002.
        testing data: mean squared error = 0.06801544 and r2 = 0.4981.
For model logistic regression with l1 regularization:
        training data: mean squared error = 0.070124454 and r2 =  0.5.
        testing data: mean squared error = 0.06801544 and r2 = 0.4981.
For model logistic regression with l2 regularization:
        training data: mean squared error = 0.070124454 and r2 =  0.5.
        testing data: mean squared error = 0.06801544 and r2 = 0.4981.

All of the models do better with the training subset than the testing subset. Let's look at which model did best of all considered: 

print(f'For independent variables:  {x_cols}:')
for mod,name in zip(pkl_models[:3],mod_names[:3]):
    print(f'For model {name}:')
    mse_tr, r2_tr = predict_using_trained_model(mod,x_tr_std,y_train)
    print(f'\ttraining data: mean squared error = {mse_tr:8.8} and r2 = {r2_tr:4.4}.')
    mse_val, r2_val = predict_using_trained_model(mod,x_te_std,y_test)
    print(f'\ttesting data: mean squared error = {mse_val:8.8} and r2 = {r2_val:4.4}.')
best_mod, best_name = best_fit(pkl_models,mod_names, x_te_std, y_test, verbose=True)
print(f'The best mode is {best_name}.')
since we had the verbose flag on, we can see the computations: 
MSE cost for model logistic regression with l1 regularization poly model: 0.068
MSE cost for model logistic regression with l2 regularization poly model: 0.068
MSE cost for model random forest with 10 number of trees poly model: 0.076
MSE cost for model random forest with 100 number of trees poly model: 0.075
MSE cost for model random forest with 1000 number of trees poly model: 0.076
MSE cost for model SVC with linear kernel poly model: 0.070
MSE cost for model SVC with poly kernel poly model: 0.075
MSE cost for model SVC with rbf kernel poly model: 0.067
MSE cost for model SVC with sigmoid kernel poly model: 0.131
The best mode is SVC with rbf kernel.

Test Suites

In Program 3 and Lecture 5, we introduced pytest. In addition to the assert statements used, we will also use parametrizations for this program. The basic format is:

The parametrize list allows you to specify the inputs and expected outputs for the function you are testing. You can define

Preceding each of these test functions, you should include @pytest.mark.parametrize list. For example, the first testing function should be of the format:

test_data = [ """TRIPLES OF DATA TO TEST GOES HERE""" ]
@pytest.mark.parametrize("test_df,test_cols,expected", test_data)
def test_impute_numeric_cols(test_df,test_cols,expected):
    assert test_impute_numeric_cols(test_df,test_cols).equals(expected)

Hints: