CSci 39542 Syllabus    Resources    Coursework

Program 9: State Migration Flows
CSci 39542: Introduction to Data Science
Department of Computer Science
Hunter College, City University of New York
Spring 2022

---

Classwork    Quizzes    Homework    Project   

---

---

Program Description

Program 9: State Migration Flows.   Due 10am, Wednesday, 29 March 19 April.
Learning Objective: to increase facility with standard linear algebra approaches for modeling data.
Available Libraries: pandas, numpy, sklearn, and core Python 3.6+.
Data Sources: State-to-State Migration Flows from the US Census.
Sample Datasets:

• State-to-State Migration Flows: 2019 .
• State-to-State Migration Flows: 2018 .
• State-to-State Migration Flows: 2017 .

In Lecture 8 and Explained Visually, we recapped matrices, eigenvectors and eigenvalues. We introducded Markov Chains with a simplified example of migration flow between California and New York:

For this program, we will use the US Census bureau's data on migration between states. The data is stored, yearly, as an excel file. We begin by extracting and cleaning the data. We will then use subsets of the data to model flows between subsets of states both after a fixed number of years and the steady state.

• import_data(file_name): This function has one input:
  • file_name: the name of a .xls file from State-to-State Migration Flows from the US Census.
  The function reads in the file (hint: use pd.read_excel) and returns a DataFrame with 51 rows: the first row for United States, as well as a row for each state, as well as the District of Columbia. The columns of the DataFrame should be arranged as:
  • All null values should be filled with 0.
  • The first column should be named Locale and contains the name of the area. The first row should be United States, followed by the states in alphabetical order: Alabama, Alaska, ..., Wymoning (following the order in the initial datasets). Note that we're leaving off Puerto Rico and the US Territories since they are not counted in the overall estimates.
  • The second column should be named Total and contains the total population for each row.
  • The third column, Stayed contains the sum of the those who stayed in the same house and same state (i.e. the sum of two columns from the initial excel file).
  • The subsequent columns contain the number of new residents to the state, by previous location. For example, the third column, Alabama contains the number of new residents to Alabama from each state. For the row Alabama, this cell (e.g. df.loc['Alabama','Alabama']) would be 0, since it's the same state. For the row Alaska, this cell, (e.g. df.loc['Alabama','Alaska']), would be the number of people who moved from Alaska to Alabama this past year. In the case of 2019 data, there were 1,105 people who previously lived in Alaska and moved to Alabama.
  • The row, United States2, has the total number of people for its first column, the number of people who didn't move, followed by the total who moved into each state.
  • All other columns, such as totals, territorial information, and repetitions of the row labels, should be dropped. The resulting DataFrame should have 52 rows and 54 columns.
  This function returns a DataFrame.


• make_transition_mx(df): This function has one input:
  • df: a DataFrame with columns, Locale, Total, Stayed, followed by states' data. The first row (for locale United States2) is ignored and the subsequent rows should contain the states in the same order as the column labels.
  Returns a transition matrix, where values range from 0 to 1, and each column sums to 1. The entries represent the fraction of the population that migrated to that state, with the diagonals being the population that stayed (didn't move).


• moving(transition_mx, starting_pop, num_years = 1): This function has three inputs and returns an array:
  • transition_mx: an square array of values between 0 and 1. Each column sums to 1.
  • starting_pop: an 1D array of positive numeric values that has the same length as transition_mx.
  • num_years: a column name containing the dependent variable (what's being predicted) in the model. It has a default value is 1.
  The function returns an array of the population of each state after num_years.


• steady_state(transition_mx, starting_pop): This function has two inputs and returns an array:
  • transition_mx: an square array of values between 0 and 1. Each row sums to 1.
  • starting_pop: an 1D array of positive numeric values that has the same length as transition_mx.
  • num_years: a column name containing the dependent variable (what's being predicted) in the model. It has a default value is 1.
  The function returns an array of the population of each state at the steady state. That is, it returns the eigenvector corresponding to the largest eigenvalue, scaled so that it's entries sum to 1, and then multiplied by the sum of the starting populations.

Let's start by importing the data. The datasets are in excel files from the State-to-State Migration Flows page at the US Census. Here's the 2019 data opened in Excel:

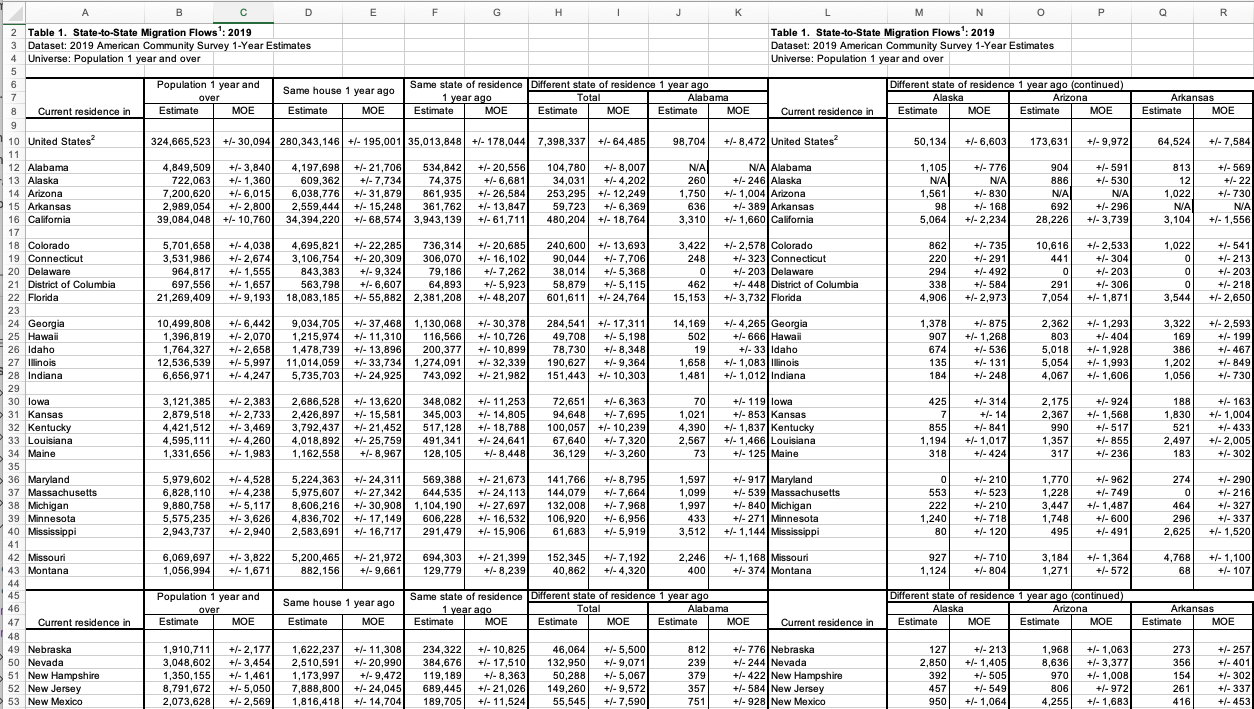
It has lots of extra rows (and columns) with notes and repeated labels that will need to be filtered out, so, will not be as simple as the importing of data in previous assignments. For this assignment, you will need to ignore the extraneous lines and columns and aggregate others. Given the large number of filtering steps, it is easiest to do this piece by piece, checking as you go, since a small discrepency early can propagate and be difficult to find later. Some useful options and commands to do this:

• When reading in files with pd.read_excel (as well as pd.read_csv), you can specify the number of lines to skip at the beginning of the file (skiprows=...) and the end of the file (skipfooter=...).
• While pd.read_csv has an option to skip empty or blank lines when reading in a file, pd.read_excel does not. So, you will need to remove those after you have read the file into the DataFrame.
• To drop all columns that contain a specific substring, a very useful command is:

  df = df.loc[:, ~df.columns.str.contains("MOE")]

  which identifies all column names that contain MOE and the ~ gives the opposite (i.e. all columns that don't contain MOE).
• While pd.read_csv has an option to skip empty or blank lines when reading in a file, pd.read_excel does not. So, you will need to remove the blank lines from the DataFrame.
• Since there are 51 columns to rename, you may find it useful to build a list of the old column labels (depending on how you drop the previous rows they will be named different things, one possibility is that they're named Estimate.4, Estimate.5, ..., Estimate.58) and a list of the locales from that column and replace using a command such as:

  df = df.rename(columns=dict(zip(old_labels,locales)))

Let's try the importing data function on the 2019 dataset:

df_2019 = import_data('State_to_State_Migrations_Table_2019.xls')
print(df_2019)

which prints:

                     Locale      Total     Stayed  Alabama  Alaska  Arizona  Arkansas  California  ...   Texas   Utah  Vermont  Virginia  Washington  West Virginia  Wisconsin  Wyoming
  0          United States2  324665523  315356994    98704   50134   173631     64524      653551  ...  453015  88426    22714    276849      199758          40460     101668    23287
  1                 Alabama    4849509    4732540        0    1105      904       813        3690  ...    8405   2083        0      2876        1883            421       1307        0
  2                  Alaska     722063     683737      260       0      886        12        2547  ...    4332   1092       44      2216        1435            355        228      242
  3                 Arizona    7200620    6900711     1750    1561        0      1022       59713  ...   17482   8917      662      3837       17636            237       3688      664
  4                Arkansas    2989054    2921206      636      98      692         0        4967  ...   12851    710        0       671         571            133        797     1109
  5              California   39084048   38337359     3310    5064    28226      3104           0  ...   37063   8504      784     24506       31882            303       4811     1159
  6                Colorado    5701658    5432135     3422     862    10616      1022       29350  ...   32295   2458      161      6796        7333            502       4454     3860
  7             Connecticut    3531986    3412824      248     220      441         0        4049  ...    2141    120      103      1764         191            408        232        0
  8                Delaware     964817     922569        0     294        0         0         161  ...     744     75        0      1260          45            219          0        0
  9   District of Columbia      697556     628691      462     338      291         0        3437  ...    2073      0       54      8828         852            324        362        0
  10                Florida   21269409   20464393    15153    4906     7054      3544       28628  ...   26174   3433     3355     26031        6870           2186       6563      624
  11                Georgia   10499808   10164773    14169    1378     2362      3322       15437  ...   22452   1182      265     11686        2879            408       3898      968
  12                 Hawaii    1396819    1332540      502     907      803       169       10954  ...    1667    772       65      3107        4322            197         83        0
  13                  Idaho    1764327    1679116       19     674     5018       386       17722  ...    3198   7371        0      1715       13505              0        620      662
  14               Illinois   12536539   12288150     1658     135     5054      1202       14692  ...    9106    326       74      5338        4364            379      12021      109
  15                Indiana    6656971    6478795     1481     184     4067      1056        7255  ...    7095    490       40      2096        2186             10       1962      118
  16                   Iowa    3121385    3034610       70     425     2175       188        5819  ...    3936      3        0      1051         781            409       4722      434
  17                 Kansas    2879518    2771900     1021       7     2367      1830        4957  ...    8374    378        0      1556        2325            174        610      442
  18               Kentucky    4421512    4309565     4390     855      990       521        3410  ...    2878   1746       95      4170        2232            983       2088        0
  19              Louisiana    4595111    4510233     2567    1194     1357      2497        4228  ...   19675    129      112      1526         805             49        529        0
  20                  Maine    1331656    1290663       73     318      317       183        1644  ...     459    161      424       307         541             11        353       88
  21               Maryland    5979602    5793751     1597       0     1770       274       10092  ...    4954   1186      368     23429        1338           4933       1790        0
  22          Massachusetts    6828110    6620142     1099     553     1228         0       11430  ...    6088   1286     2167      3768        2353             63        281      154
  23               Michigan    9880758    9710406     1997     222     3447       464        8672  ...    8434    428       32      3468        1726            767       4361      139
  24              Minnesota    5575235    5442930      433    1240     1748       296        6232  ...    5916    314        0      1743        5166              0      18403      207
  25            Mississippi    2943737    2875170     3512      80      495      2625        3024  ...    4689    406       10      2244         526            647       1146        0
  26               Missouri    6069697    5894768     2246     927     3184      4768        7970  ...   11507   1567     1094      2682        2903            829       3004       45
  27                Montana    1056994    1011935      400    1124     1271        68        5298  ...     780   1900      134       768        4907            176        107     1662
  28               Nebraska    1910711    1856559      812     127     1968       273        2035  ...    4199   1111        0      1180         365            148        725     1000
  29                 Nevada    3048602    2895267      239    2850     8636       356       47322  ...    5240   6593        0      1959        3906             74       1156       46
  30          New Hampshire    1350155    1293186      379     392      970       154        1110  ...     892    272     2370       890         582            155        621        0
  31             New Jersey    8791672    8578245      357     457      806       261        9155  ...    4489    540      133      4810         996            494        308        0
  32             New Mexico    2073628    2006123      751     950     4255       416        5915  ...   15762    766      102       564        1330              0        142     1451
  33               New York   19240920   18851752      851     596     2185      1130       24332  ...   13033   1185     3084     12180        2697            530       1450       72
  34         North Carolina   10371906   10004581     4697    1568     5319      1976       18023  ...   14226   1125      435     29764        2984           2950       1643      161
  35           North Dakota     750501     709863        0     214      945        46         404  ...    3075    444        0       302        1759              0        313      730
  36                   Ohio   11556037   11306918     1203     468     3591      1195       12277  ...   13564   2629      582      5339        2155           6056       3490      492
  37               Oklahoma    3907258    3791883      241     188     2962      7421        7408  ...   26383    155      363      2146        2039            216         64      326
  38                 Oregon    4178578    4028858      162    2068     6540       425       37927  ...    4441   3684      298      1582       21339              0        564      680
  39           Pennsylvania   12670245   12351358     1898    1008     3104       502       13048  ...   11490    869     1483     12193        2394           3763        942       24
  40           Rhode Island    1050602    1011092        0       0      423         0        1854  ...    1597    186      428       863         144             83        136        0
  41         South Carolina    5092727    4893662      873     680     1704       579        7785  ...    7631    548      336     10143        2112           1559       1702        0
  42           South Dakota     872708     841142      339      14      650       141        1778  ...    1080    199        0        76         280              0        391      473
  43              Tennessee    6754461    6537328     6294    1506     1457      5252       11874  ...   15068   1240      336      8040        3821           1235       1188       46
  44                  Texas   28642658   27865912     8791    4622    21205     12341       82235  ...       0  10072      445     18973       15128           1059       4824     1311
  45                   Utah    3162102    3050711     1027     526     6301       888       17821  ...    4871      0      233       922        4481            322        547     1549
  46                Vermont     617560     594528       77     402       41         0        1048  ...    1082     41        0       527         413             20          0       30
  47               Virginia    8439982    8105540     4028    1256     2513      1011       16994  ...   13924   1736     1633         0        6580           5518       1518      167
  48             Washington    7527366    7231397     1060    4255     8263        83       46791  ...   18528   5440      391      6656           0            275       1456      626
  49          West Virginia    1773280    1728350      245     192      356       120         940  ...     927      0       19      6008         129              0         41        0
  50              Wisconsin    5760481    5635872      678    1070     1917       290        6886  ...    5049    808        0      1878        1682            572          0     1417
  51                Wyoming     572884     541255     1227      54      757       298        3211  ...    1696   1746        0       415         885            308         27        0
  
  [52 rows x 54 columns]

Let's try the importing data function on the 2019 dataset:

tr_mx = make_transition_mx(df_2019)
  print(tr_mx)

which prints:

[[9.71328865e-01 2.27858119e-04 1.86410624e-04 ... 8.68129124e-05
  2.69511821e-04 0.00000000e+00]
[3.60079384e-04 9.75880239e-01 1.22703975e-03 ... 4.91646851e-04
3.15761921e-04 3.35150811e-04]
[2.43034628e-04 2.16786888e-04 9.46921529e-01 ... 3.29138324e-05
5.12178118e-04 9.22142815e-05]
...
[1.38162050e-04 1.08273933e-04 2.00757918e-04 ... 9.60680934e-01
2.31209961e-05 0.00000000e+00]
[1.17698505e-04 1.85748378e-04 3.32784710e-04 ... 9.92972635e-05
9.74662772e-01 2.45986403e-04]
[2.14179485e-03 9.42599200e-05 1.32138443e-03 ... 5.37630655e-04
4.71299600e-05 9.78368299e-01]]

Let's pare the matrix down to just California, New York, and a catch-all category for all other states:

df_ca_ny = df_2019[ ['Locale','Total','Stayed','California','New York'] ]
df_ca_ny = df_ca_ny[ df_ca_ny['Locale'].isin(['United States2','California','New York']) ]
print(df_ca_ny)
tr_mx_ca_ny = make_transition_mx(df_ca_ny)
np.set_printoptions(precision=3, suppress=True)
print(tr_mx_ca_ny)
other = np.ones(2) - (tr_mx_ca_ny[0]+tr_mx_ca_ny[1])
tr_mx_ca_ny = np.concatenate((tr_mx_ca_ny,[other]),axis=0)
other_2_ny = (df_ca_ny.iloc[2,1]-(df_ca_ny.iloc[2,2]+df_ca_ny.iloc[2,3]))/df_ca_ny.iloc[2,1]
other_2_ca = (df_ca_ny.iloc[1,1]-(df_ca_ny.iloc[1,2]+df_ca_ny.iloc[1,3]))/df_ca_ny.iloc[2,1]
other_2_other = 1.0 - (other_2_ca + other_2_ny)
others = np.array([[other_2_ca], [other_2_ny], [other_2_other]])
tr_mx_ca_ny = np.append(tr_mx_ca_ny,others,axis=1)
print(tr_mx_ca_ny)

which prints:

            Locale      Total     Stayed  California  New York
0   United States2  324665523  315356994      653551    439708
5       California   39084048   38337359           0     37567
33        New York   19240920   18851752       24332         0
[[0.971 0.001]
  [0.001 0.981]]
[[0.971 0.001 0.039]
  [0.001 0.981 0.019]
  [0.027 0.018 0.942]]

In words, we have:

• Californians:
  • 97.1% of Californians stay in California.
  • 0.1% of Californians move to New York.
  • 2.7% of Californians move to another state (besides NY).
• New Yorkers:
  • 98.1% of New Yorkers stay in New York.
  • 0.1% of New Yorkers move to California.
  • 1.8% of New Yorkers move to another state (besides CA).
• Others:
  • 94.2% of those from other states stay in other states.
  • 3.9% of those in other states move to California.
  • 1.9% of those in other states move to New York .

Here's another example, using larger migration flows to make the patterns easier to see. If you have that people move from the following three states with the probabilities of moving each year:

• New Yorkers:
  • 70% of New Yorkers stay in New York
  • 25% of New Yorkers move to California
  • 5% of New Yorkers move to other states (not New York)
• Californians:
  • 7% of Californians move to New York
  • 90% of Californians stay in California
  • 3% of Californians move to other states (not California)
• Other states:
  • 10% of other staters move to New York
  • 15% of other staters move to California
  • 75% of other staters stay in other states

If the initial populations are New York: 20 million, California: 40 million, and Texas: 25 million. Then, the transition matrix is:

t_mx = np.array([[.7, .07, .1],
   [.25,.9,.15],
   [.05,.03,.75]])

and the starting populations (in millions) are: pop0 = np.array([20, 40, 25]) we can compute the population after 1 years, by taking the intial populations, computing what fraction move to each of the other states:

pop1 = t_mx @ pop0
print(f'Population of each state after 1 year: {pop1}.')

which is

Population of each state after 1 year: [19.3  44.75 20.95].

Similarly, the population after 2 years, can be found by multiplying the population after 1 year by the transition matrix. More generally, the population after k+1 years can be found by multiplying the populations at year k by the transition matrix. The steady state population can be found by first finding the eigenvector corresponding to the maximal eigenvalue of 1, scaling it so its entries sum to 1 (i.e. divide through by its sum) to get percentages. And then, multiplying the percentages by the total population.

For example, continuing from above, and assuming your functions are in p43 and the appropriate libraries are loaded:

pop1 = moving(t_mx, pop0)
print(f'Population of each state after 1 year: {pop1}')
pop100 = p43.moving(t_mx, pop0, num_years=100)
print(f'Population of each state after 100 years: {pop1}')
pop_steady = p43.steady_state(t_mx, pop0)
print(f'Steady state population: {pop_steady}')

and print:

Population of each state after 1 year: [19.3  44.75 20.95]
Population of each state after 100 years: [16.91747573 57.76699029 10.31553398]
Steady state population: [16.91747573 57.76699029 10.31553398]

Note: you should submit a file with only the standard comments at the top, this function, and any helper functions you have written. The grading scripts will then import the file for testing.

Hints:

• The make_transition_mx function returns a 2D numpy array. To create it, there are several functions that may be useful:
  • pd.div allows you to divide every entry in a pandas DataFrame by a column.
  • pd.to_numpy converts a pandas DataFrame of numeric values into a numpy array.
  • np.fill_diagonal is useful for filling the diagonal entries of the transition matrix with the fraction of people who stayed in the state.
• The module numpy has many useful functions for computing determinants and eigenvalues in its linear algebra package. Note that the * for matrices is element-wise (not regular matrix multiplication). To multiply two matrices, a and b together use a @ b.
• A useful function to raise a matrix to a power, is numpy.linalg.matrix_power described in the numpy API reference.
• The numpy.linalg.eig function returns an array of eigenvalues and the associated eigenvectors as columns of an array. For the example above,

  import numpy.linalg as LA
  w,v = LA.eig(t_mx)
  print(f'The eigenvalues are: {w} and eigenvectors are:\n{v}.')

  would print:

  The eigenvalues are: [ 1.  -0.2  0.1] and eigenvectors are:
  [[-6.67423812e-01 -7.07106781e-01  2.67261242e-01]
  [-5.72077554e-01  6.87552368e-17 -8.01783726e-01]
  [-4.76731295e-01  7.07106781e-01  5.34522484e-01]].

  The eigenvector for eigenvalue = 1 is the first column (not the first row-- the rows are grouped together since we enter/print 2D arrays by rows).