CSci 39542 Syllabus    Resources    Coursework


Program 6: Taxi Tips
CSci 39542: Introduction to Data Science
Department of Computer Science
Hunter College, City University of New York
Spring 2023

Classwork    Quizzes    Homework    Project   

Program Description


Program 6: Taxi Tips.   Due 10am, Wednesday, 8 March.
Learning Objective: give students practice on implementing model from start to finish and to strengthen understanding of model drift.
Available Libraries: pandas, numpy, datetime, pickle, sklearn, and core Python 3.6+.
Data Sources: Yellow Taxi Trip Data and NYC Taxi Zones from OpenData NYC.
Sample Datasets: taxi_new_years_day_2020.csv, taxi_4July2020.csv, taxi_jfk_june2020.csv, and taxi_zones.csv.

image of yellow taxi

This program is tailored to the NYC OpenData Yellow Taxi Trip Data and follows astandard strategy for data cleaning and model building of:

  1. Read in datasets, merging and cleaning as needed.
  2. Impute missing values (we will use median for the numeric values and one-hot encoding for categorical values).
  3. Transform features to polynomial (we will restrict to quadratic).
  4. Split our dataset into training and testing sets.
  5. Fit a model, or multiple models, to the training dataset.
  6. Validate the models using the testing dataset.
This program will focus on building a linear regression model on the features of our dataset to predict tip percentages.

The function specifications are:

For example, the file, taxi_jfk_june2020.csv, contains all taxi trips, starting from JFK in June 2020 Yellow Taxi Trip Data (about 9,500 entries) with the first lines are: 

VendorID,tpep_pickup_datetime,tpep_dropoff_datetime,passenger_count,trip_distance,RatecodeID,store_and_fwd_flag,PULocationID,DOLocationID,payment_type,fare_amount,extra,mta_tax,tip_amount,tolls_amount,improvement_surcharge,total_amount,congestion_surcharge
2,06/01/2020 12:00:31 AM,06/01/2020 12:31:43 AM,1,12.59,1,N,132,189,2,37,0.5,0.5,0,0,0.3,38.3,0
2,06/01/2020 12:05:23 AM,06/01/2020 12:29:05 AM,1,15.8,1,N,132,255,1,42,0.5,0.5,8.66,0,0.3,51.96,0
2,06/01/2020 12:06:27 AM,06/01/2020 12:36:26 AM,1,18.19,2,N,132,142,1,52,0,0.5,10,0,0.3,65.3,2.5
2,06/01/2020 12:08:48 AM,06/01/2020 12:40:48 AM,2,19,2,N,132,113,1,52,0,0.5,13.82,0,0.3,69.12,2.5
2,06/01/2020 12:13:46 AM,06/01/2020 12:25:29 AM,1,7.21,1,N,132,134,2,21,0.5,0.5,0,0,0.3,22.3,0
Then our first functions: 
df = import_data('taxi_jfk_june2020.csv')
df = add_tip_time_features(df)
print(df[ ['trip_distance','duration','dayofweek','total_amount','percent_tip'] ].head() )
prints: 
   trip_distance  duration  dayofweek  total_amount  percent_tip
0          12.59    1872.0          0         38.30     0.000000
1          15.80    1422.0          0         51.96    20.000000
2          18.19    1799.0          0         65.30    18.083183
3          19.00    1920.0          0         69.12    24.990958
4           7.21     703.0          0         22.30     0.000000

We can impute the missing data in numerical columns with their median value. For example: 

print(df[ ['passenger_count','trip_distance'] ].head(10) )
df = impute_numeric_cols(df)
print( df[ ['passenger_count','trip_distance'] ].head(10) )
shows the passenger_count the results of impute_numeric_cols: 
   passenger_count  trip_distance
0              1.0          12.59
1              1.0          15.80
2              1.0          18.19
3              2.0          19.00
4              1.0           7.21
5              1.0           6.50
6              2.0          13.90
7              NaN           0.00
8              NaN           0.00
9              NaN           0.00
  passenger_count  trip_distance
0              1.0          12.59
1              1.0          15.80
2              1.0          18.19
3              2.0          19.00
4              1.0           7.21
5              1.0           6.50
6              2.0          13.90
7              1.0           0.00
8              1.0           0.00
9              1.0           0.00

The running example in the textbook focuses on predicting restaurant tips. A highly correlated feature with tips for restaurant meals is the total bill. Let's look at the taxi data set to see if a similar correlation is suggested for tips on yellow taxi trips: 

#Explore some data:
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_theme(color_codes=True)

sns.lmplot(x="total_amount", y="percent_tip", data=df)
tot_r = df['total_amount'].corr(df['percent_tip'])
plt.title(f'Taxi Trips from JFK, June 2020 with r = {tot_r:.2f}')
plt.tight_layout()  #for nicer margins
plt.show()
sns.lmplot(x="trip_distance", y="percent_tip", data=df)
dist_r = df['trip_distance'].corr(df['percent_tip'])
plt.title(f'Taxi Trips from JFK, June 2020 with r = {dist_r:.2f}')
plt.tight_layout()  #for nicer margins
plt.show()

The resulting images:

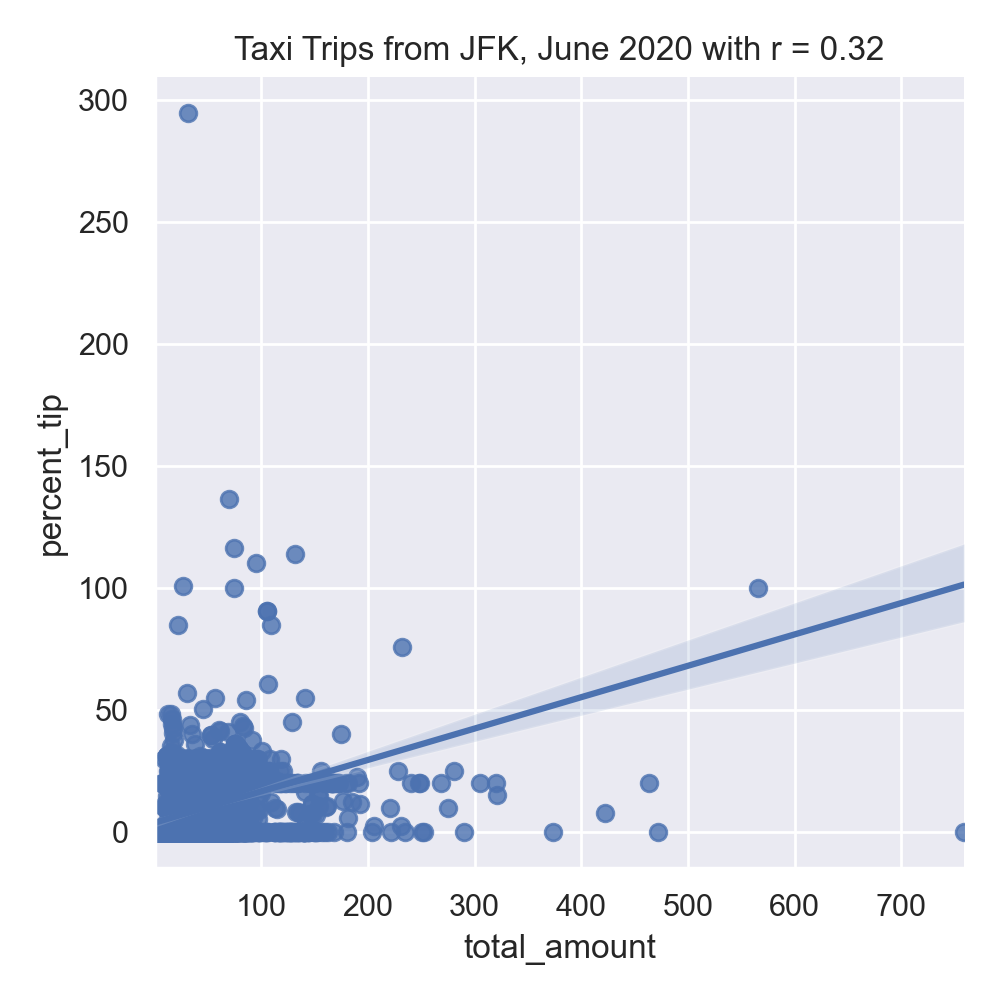
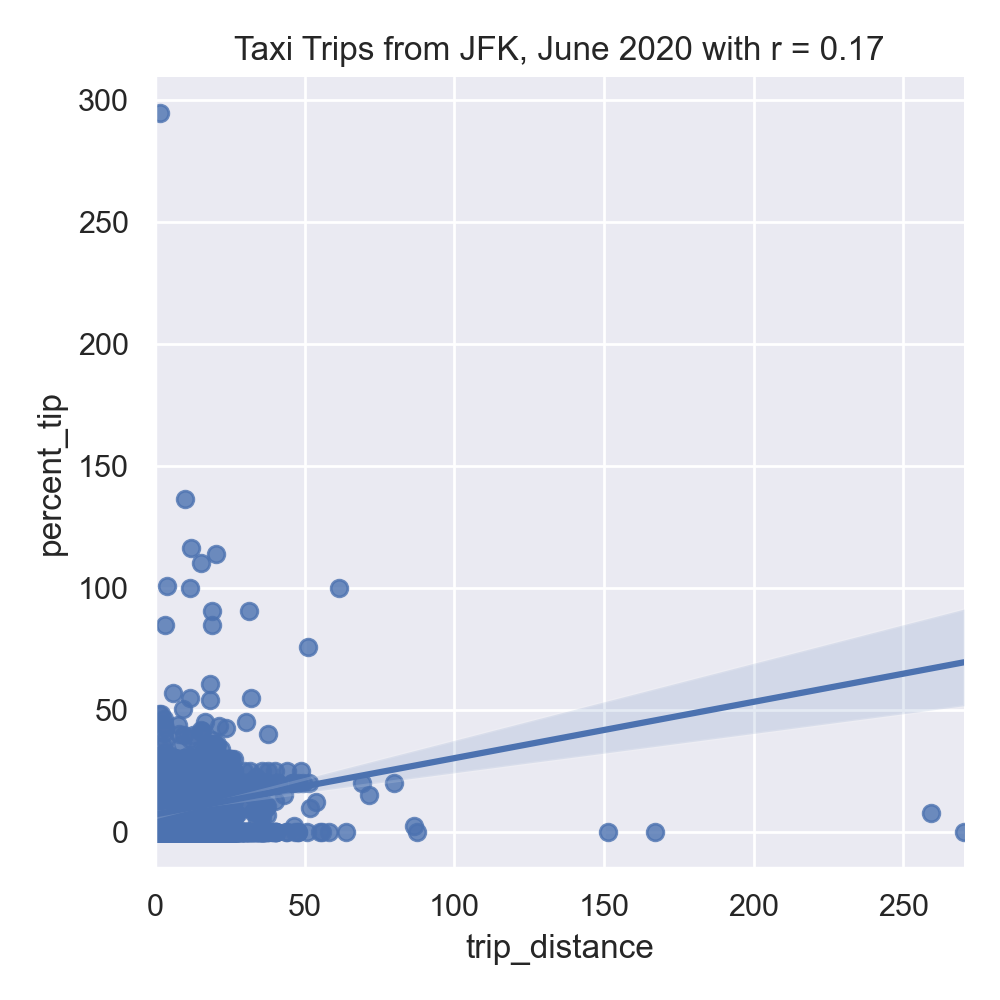
Neither total amount or distance of the trip are strongly correlated, suggesting a linear regression model with a single input will not make a good predictor.

Next, let's use our new functions to add in boroughs for the pick up and drop off locations 

df = add_boro(df,'taxi_zones.csv')
print('\nThe locations and borough columns:')
print(f"{df[['PULocationID','PU_borough','DOLocationID','DO_borough']]}")

which prints out the new columns: 

The locations and borough columns:
      PULocationID PU_borough  DOLocationID DO_borough
0              132     Queens           189   Brooklyn
1              132     Queens           255   Brooklyn
2              132     Queens           142  Manhattan
3              132     Queens           113  Manhattan
4              132     Queens           134     Queens
...            ...        ...           ...        ...
9495           132     Queens            36   Brooklyn
9496           132     Queens           263  Manhattan
9497           132     Queens           132     Queens
9498           132     Queens            75  Manhattan
9499           132     Queens           249  Manhattan

[9500 rows x 4 columns]
And encode the categorical columns for drop off boroughs so we can use them as inputs for our model: 
df_do = encode_categorical_col(df['DO_borough'],'DO_')
print(df_do.head())

The first few lines of the resulting DataFrames: 

     DO_Bronx  DO_Brooklyn  DO_EWR  DO_Manhattan  DO_Queens
  0         0            1       0             0          0
  1         0            1       0             0          0
  2         0            0       0             1          0
  3         0            0       0             1          0
  4         0            0       0             0          1

Let's combine all the DataFrames into one (using concat along column axis): 

df_all = pd.concat( [df,df_do], axis=1)
print(f'The combined DataFrame has columns: {df_all.columns}')

The combined DataFrame has the columns: 

The combined DataFrame has columns: Index(['tpep_pickup_datetime', 'tpep_dropoff_datetime', 'passenger_count',
    'trip_distance', 'PULocationID', 'DOLocationID', 'fare_amount',
    'tip_amount', 'total_amount', 'percent_tip', 'duration',
    'dayofweek', 'PU_borough', 'DO_borough', 'DO_Bronx', 'DO_Brooklyn',
    'DO_EWR', 'DO_Manhattan', 'DO_Queens'],
   dtype='object')
Let's build a more complicated model that uses multiple inputs, including the numerical and encoded categorical columns: 
df_all = impute_numeric_cols(df_all)
num_cols = ['passenger_count','trip_distance','fare_amount',\
'tip_amount', 'total_amount', 'percent_tip', 'duration','dayofweek',\
'PU_borough', 'DO_borough', 'DO_Bronx', 'DO_Brooklyn','DO_EWR',\
'DO_Manhattan', 'DO_Queens']

With the missing numeric data imputed, we can fit the model on training sets (of size 25%): 

x_train,x_test,y_train,y_test = split_test_train(df_all,num_cols, 'percent_tip')
  print('For numeric columns, training on 25% of data:')
  mod_pkl = fit_linear_regression(x_train,y_train)
  mod = pickle.loads(mod_pkl)
  print(f'intercept = {mod.intercept_} and coefficients = {mod.coef_}')
  tr_err,tr_r2 = predict_using_trained_model(mod_pkl, x_train,y_train)
  print(f'training:  RMSE = {tr_err} and r2 = {tr_r2}.')
  test_err,test_r2 = predict_using_trained_model(mod_pkl, x_test,y_test)
  print(f'testing:  RMSE = {test_err} and r2 = {test_r2}.')

the resulting model does a reasonable both with the training and testing data sets that we used to validate the model: 

For numeric columns, training on 25% of data:
intercept = -4.796163466380676e-14 and coefficients = [ 5.23397910e-17  1.61192577e-15  1.85687045e-16 -5.56734918e-17
  -2.61963848e-16  1.00000000e+00  1.31317482e-17  1.22153806e-16
  -1.72760552e-15  2.32202615e-16 -9.61810652e-17 -3.20366914e-17
  -5.19491682e-17]
training:  RMSE = 1.7731188666093563e-27 and r2 = 1.0.
testing:  RMSE = 2.2870524510872717e-27 and r2 = 1.0.

Let's do the same with just two of the columns: 

x_train,x_test,y_train,y_test = split_test_train(df_all,num_cols, 'percent_tip')
print('For numeric columns, training on 25% of data:')
mod_pkl = fit_linear_regression(x_train,y_train)
mod = pickle.loads(mod_pkl)
print(f'intercept = {mod.intercept_} and coefficients = {mod.coef_}')
tr_err,tr_r2 = predict_using_trained_model(mod_pkl, x_train,y_train)
print(f'training:  RMSE = {tr_err} and r2 = {tr_r2}.')
test_err,test_r2 = predict_using_trained_model(mod_pkl, x_test,y_test)
print(f'testing:  RMSE = {test_err} and r2 = {test_r2}.')

the resulting model does a reasonable both with the training and testing data sets that we used to validate the model: 

For ['duration','total_amount'], training on 25% of data:
intercept = -4.796163466380676e-14 and coefficients = [ 5.23397910e-17  1.61192577e-15  1.85687045e-16 -5.56734918e-17
-2.61963848e-16  1.00000000e+00  1.31317482e-17  1.22153806e-16
-1.72760552e-15  2.32202615e-16 -9.61810652e-17 -3.20366914e-17
-5.19491682e-17]
training:  RMSE = 117.29525461464237 and r2 = 0.09393010147197978.
testing:  RMSE = 106.48541736076493 and r2 = 0.12955509236760188.

Neither does very well, compared to using all the possible columns.

We can use the model for other yellow taxi data sets to see how well our model does: 

print(f'Prediction for 4 July data with only duration and total amount:')
df_july = import_data('program06/taxi_4July2020.csv')
df_july = add_tip_time_features(df_july)
df_july = impute_numeric_cols(df_july)
print(df_july[['duration','total_amount']])
july_err,july_r2 = predict_using_trained_model(mod2_pkl, df_july[['duration','total_amount']].to_numpy(),df_july['percent_tip'])
print(f'RMSE = {july_err} and r2 = {july_r2}.')

The restricted model does not do well with the other data set: 

Prediction for 4 July data:
RMSE = 441.3910670031561 and r2 = -0.060720824296001785.

While the full model does quite well predicting results for other data sets: 

print(f'Prediction for 4 July data with full model:')
df_july = add_boro(df_july,'program06/taxi_zones.csv')
df_do_j = encode_categorical_col(df_july['DO_borough'],'DO_')
df_all_j = pd.concat( [df_july,df_do_j], axis=1)
july_err,july_r2 = predict_using_trained_model(mod_pkl, df_all_j[num_cols].to_numpy(),df_all_j['percent_tip'])
print(f'RMSE = {july_err} and r2 = {july_r2}.')
Prediction for 4 July data with full model:
RMSE = 3.2743379800535055e-27 and r2 = 1.0.

Notes and Hints: