CSci 39542 Syllabus    Resources    Coursework

Program 11: EMS Stations
CSci 39542: Introduction to Data Science
Department of Computer Science
Hunter College, City University of New York
Spring 2022

---

Classwork    Quizzes    Homework    Project   

---

---

Program Description

Program 11: EMS Stations.   Due 10am, Wednesday, 26 April.
Learning Objective: to enhance data cleaning skills and build understanding of clustering algorithms.
Available Libraries: pandas, datetime, numpy, sklearn, and core Python 3.6+.
Data Sources: 911 System Calls (NYC OpenData)
Sample Datasets:

• Small dataset (1 day of calls for 1 borough): NYPD_Calls_Manhattan_4Jul2021.csv,
• Midnight calls in January 2021 (all boroughs): NYPD_Calls_midnight_Jan2021.csv,
• Larger dataset (1 month of calls for Queens): NYPD_Calls_Queens_Jan2021.csv

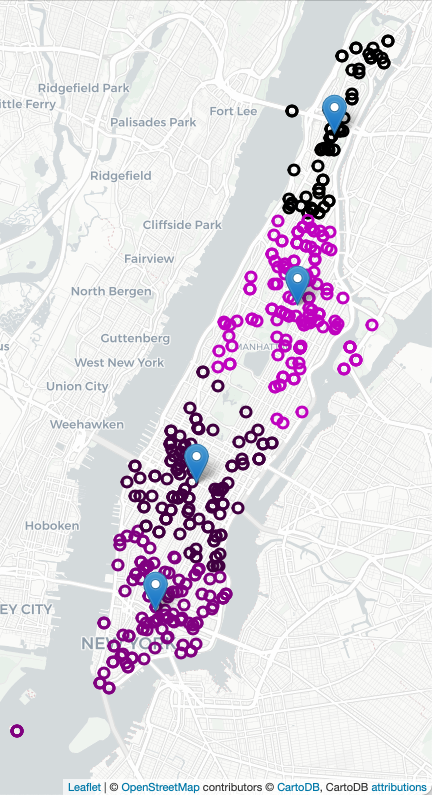
For this program, we are building on Classwork 10 which focused ambulance calls in New York City. Decreasing ambulance response times improves outcomes and strategic placement of ambulance stations and overall allocation has been shown an effective approach. For example, here are all the calls for ambulances on 4 July 2021 in Manhattan (using Folium/Leaflet to create an interactive map):

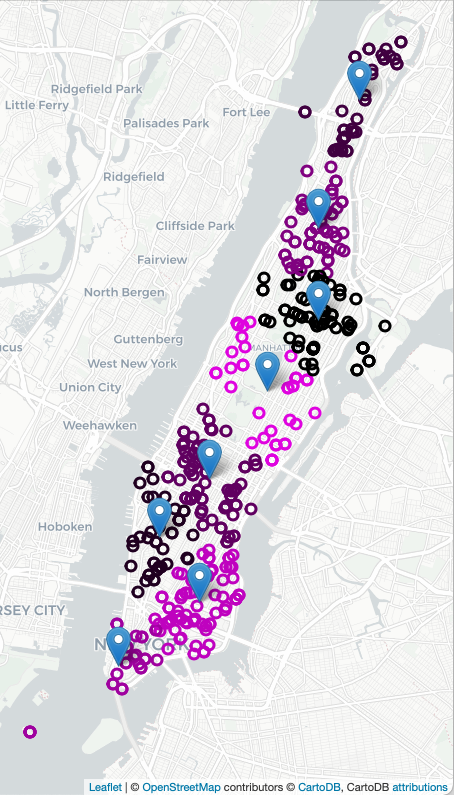
To decide on where to "pre-place" ambulances, we will use K-means clustering, where "K" is the number of ambulances available for that shift. For example, if there 2 ambulances available to be placed in Manhattan, we will look at previous ambulance calls for that shift and form 2 clusters and station each ambulance at the mean of the cluster. If two more ambulances become available, we can recompute the K-means algorithm for K=4, and place those 4 ambulances, each at the mean of the cluster found, and similarly for K=8:

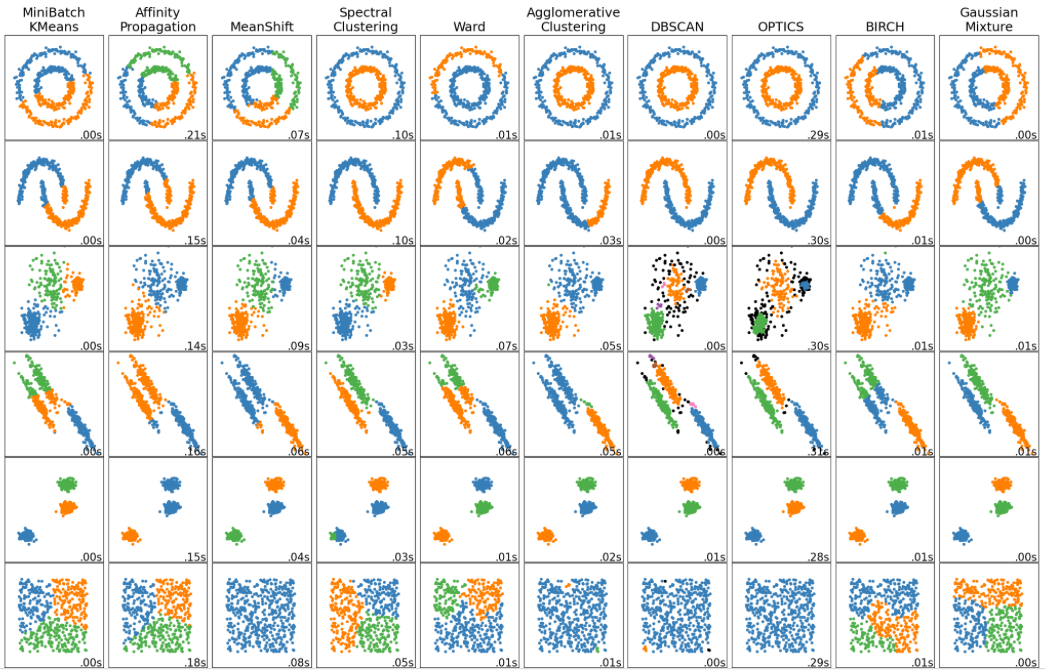
In addition to K-means analysis, we will also use standard approaches from sklearn as well as filter data by time and day.

The assignment is broken into the following functions to allow for unit testing:

• make_df(file_name): This function takes one input:
  • file_name: the name of a CSV file containing 911 System Calls from OpenData NYC.
  The data is read into a DataFrame. Rows that are have null values for the type description, incident date, incident time, latitute and longitude are dropped. Only rows that contain AMBULANCE as part of the TYP_DESC are kept. The resulting DataFrame is returned.
  Hint: see DS 100: Chapter 13 for using string methods within pandas.
  See Classwork 9.
  
  
• add_date_time_features(df): This function takes one input:
  • df: a DataFrame containing 911 System Calls from OpenData NYC created by make_df.
  An additional column WEEK_DAY is added with the day of the week (0 for Monday, 1 for Tuesday, ..., 6 for Sunday) of the date in INCIDENT_DATE is added. Another column, INCIDENT_MIN, that takes the time from INCIDENT_TIME and stores it as the number of minutes since midnight. The resulting DataFrame is returned.
  Hint: see Lecture 3 for using datetime methods with pandas, including computing the day of the week (of datetime objects) and the total seconds (of timedelta objects).
  
  
• filter_by_time(df, days=None, start_min=0, end_min=1439): This function takes four inputs:
  • df: a DataFrame containing 911 System Calls from OpenData NYC.
  • days: a list of integers ranging from 0 to 6, representing the days of the week. The default value is None and is equivalent to the list containing all days: [0,1,2,3,4,5,6].
  • start_min: a non-negative integer value representing the starting time. With end_min, it representing the range, inclusive, for the time, in minutes, that should be selected. The default value give the range of [0,1439] which ranges from midnight (0 minutes) to (1439 representing 23:59 since 23 hours + 59 minutes = 23*60+59 minutes = 1439 minutes).
  • end_min: a non-negative integer value representing the ending time. With start_min, it representing the range, inclusive, for the time, in minutes, that should be selected. The default value give the range of [0,1439] which ranges from midnight (0 minutes) to (1439 representing 23:59 since 23 hours + 59 minutes = 23*60+59 minutes = 1439 minutes).
  Returns a DataFrame with entries restricted to weekdays in days (or all weekdays if None is given) and incident times in [start_min, end_min] inclusive (e.g. contains the endpoints).
  
  
• compute_kmeans(df, num_clusters = 8, n_init = 'auto', random_state = 2022): This function takes four inputs:
  • df: a DataFrame containing 911 System Calls from OpenData NYC.
  • n_init: Number of times the k-means algorithm is run with different centroid seeds. The final results is the best output of n_init consecutive runs in terms of inertia. The default value is auto.
  • num_clusters: an integer representing the number of clusters. The default value is 8.
  • random_state: the random seed used for KMeans. The default value is 2022.
  Runs the KMeans model with num_clusters on the latitude and longitude data of the provided DataFrame. Returns the cluster centers and predicted labels computed via the model.
  A similar, but not identical function was part of Classwork 9.
  
  
• compute_gmm(df, num_clusters = 8, random_state = 2022): This function takes three inputs:
  • df: a DataFrame containing 911 System Calls from OpenData NYC.
  • num_clusters: an integer representing the number of clusters. The default value is 8.
  • random_state: the random seed used for GaussianMixture. The default value is 2022.
  Runs the GaussianMixture model with num_clusters on the latitude and longitude data of the provided DataFrame. Returns the array of the predicted labels computed via the model.
  
  
• compute_agglom(df, num_clusters = 8, linkage='ward'): This function takes three inputs:
  • df: a DataFrame containing 911 System Calls from OpenData NYC.
  • num_clusters: an integer representing the number of clusters. The default value is 8.
  • linkage: the linkage criterion used determining distances between sets for AgglomerativeClustering. The default value is 'ward'.
  Runs the Agglomerative model with num_clusters on the latitude and longitude data of the provided DataFrame and default linkage (i.e. ward). Returns the array of the predicted labels computed via the model.
  
  
• compute_explained_variance(df, K =[1,2,3,4,5], random_state = 55): This function takes three inputs:
  • df: a DataFrame containing 911 System Calls from OpenData NYC.
  • K: a list of integers representing values for the number of clusters. The default value is [1,2,3,4,5].
  • random_state: the random seed used for KMeans. The default value is 55.
  Returns a list of the sum of squared distances of samples to their closest cluster center for each value of K. This can be computed manually or via the inertia_ attribute of the KMeans model.

For example, if we use the small dataset from 4 July 2021:

df = make_df('NYPD_Calls_Manhattan_4Jul2021.csv')
print(df[['INCIDENT_TIME','TYP_DESC','Latitude','Longitude']])

would print:

     INCIDENT_TIME                             TYP_DESC   Latitude  Longitude
7         00:01:51      AMBULANCE CASE: CARDIAC/OUTSIDE  40.724578 -73.992519
27        00:06:12       AMBULANCE CASE: CARDIAC/INSIDE  40.807719 -73.964240
51        00:12:12      AMBULANCE CASE: SERIOUS/TRANSIT  40.732019 -74.000734
53        00:12:38           AMBULANCE CASE: EDP/INSIDE  40.789348 -73.947352
54        00:12:38           AMBULANCE CASE: EDP/INSIDE  40.789348 -73.947352
...            ...                                  ...        ...        ...
5175      23:50:02         AMBULANCE CASE: WATER RESCUE  40.711839 -74.011234
5176      23:50:02         AMBULANCE CASE: WATER RESCUE  40.711839 -74.011234
5205      23:57:11  AMBULANCE CASE: UNCONSCIOUS/TRANSIT  40.732019 -74.000734
5211      23:57:59           AMBULANCE CASE: EDP/INSIDE  40.827547 -73.937461
5212      23:57:59           AMBULANCE CASE: EDP/INSIDE  40.827547 -73.937461

[459 rows x 4 columns]

Note that the original CSV file had over 5000 lines, only 459 of those were for ambulances calls. The indices were not reset and refer to the line numbers of the original file.

Let's add in the date and time features:

df = add_date_time_features(df)
print(df[['INCIDENT_DATE','WEEK_DAY','INCIDENT_TIME','INCIDENT_MIN']])

would print:

     INCIDENT_DATE  WEEK_DAY INCIDENT_TIME  INCIDENT_MIN
7       07/04/2021         6      00:01:51      1.850000
27      07/04/2021         6      00:06:12      6.200000
51      07/04/2021         6      00:12:12     12.200000
53      07/04/2021         6      00:12:38     12.633333
54      07/04/2021         6      00:12:38     12.633333
...            ...       ...           ...           ...
5175    07/04/2021         6      23:50:02   1430.033333
5176    07/04/2021         6      23:50:02   1430.033333
5205    07/04/2021         6      23:57:11   1437.183333
5211    07/04/2021         6      23:57:59   1437.983333
5212    07/04/2021         6      23:57:59   1437.983333

[459 rows x 4 columns]
[Finished in 2.294s]

Since all the incidents are from a single day (i.e. 4 July 2021) the WEEK_DAY column has the same value (i.e. 6) for every row.

Let's add in the date and time features:

df_early_am = filter_by_time(df,times=[0,360])
print(df_early_am[['INCIDENT_DATE','WEEK_DAY','INCIDENT_TIME','INCIDENT_MIN']])

would print:

     INCIDENT_DATE  WEEK_DAY INCIDENT_TIME  INCIDENT_MIN
7       07/04/2021         6      00:01:51      1.850000
27      07/04/2021         6      00:06:12      6.200000
51      07/04/2021         6      00:12:12     12.200000
53      07/04/2021         6      00:12:38     12.633333
54      07/04/2021         6      00:12:38     12.633333
...            ...       ...           ...           ...
1041    07/04/2021         6      05:08:49    308.816667
1068    07/04/2021         6      05:21:49    321.816667
1075    07/04/2021         6      05:24:21    324.350000
1079    07/04/2021         6      05:28:13    328.216667
1111    07/04/2021         6      05:41:34    341.566667

[76 rows x 4 columns]

We can build a map with the calls for ambulances shaded by the time of the call:

import folium
import matplotlib.colors
def cc(minute,scale):
    return(matplotlib.colors.to_hex( (minute/scale,0,minute/scale) ))

m = folium.Map(location=[40.7678,-73.9645],zoom_start=13,tiles="cartodbpositron")
df.apply( lambda row: folium.CircleMarker(location=[row["Latitude"], row["Longitude"]],
                                        radius=5, popup=(row['INCIDENT_TIME']+": "+row['TYP_DESC']),
                                        color=cc(row['INCIDENT_MIN'],2000))
                                        .add_to(m) ,
        axis=1)
m.save('4_July_map.html')

displayed at the top of the page. Note that we used the time to shade the incidents. The popups provide the exact time as well as the description.

We can also make maps with the computed clusters. We use the compute_locations function with different values of num_clusters. Since we are repeating the same actions for K = 2, 4, 6, we wrote a helper function to create the HTML maps:

def make_map(df, num_clusters, out_file):
    centers,labels = compute_kmeans(df,num_clusters = num_clusters)
    df_map = df[ ['Latitude','Longitude','INCIDENT_TIME','INCIDENT_MIN','TYP_DESC'] ]
    df_map = df_map.assign(Labels = labels)
    m = folium.Map(location=[40.7678,-73.9645],zoom_start=13,tiles="cartodbpositron")
    df_map.apply( lambda row: folium.CircleMarker(location=[row["Latitude"], row["Longitude"]],
                                        radius=5, popup=(row['INCIDENT_TIME']+": "+row['TYP_DESC']),
                                        color=cc(row['Labels'],num_clusters))
                                        .add_to(m), axis=1)
    for i in range(num_clusters):
        x,y = centers[i]
        folium.Marker(location=[x,y],popup = "Cluster "+str(i)).add_to(m)
    m.save(out_file)

make_map(df,2,'map_4_July_2clusters.html')
make_map(df,4,'map_4_July_4clusters.html')
make_map(df,8,'map_4_July_8clusters.html')

Screenshots of the maps are displayed above.

Another function can be used to filter the dataset by day of the week and time of day. For example, still working with the 4 July data set:

df_mondays = filter_by_time(df, days = [0])
print(df_mondays)

This will return an empty DataFrame since only 4 of July in this data set (which was a Sunday and we filtered for 0 or Monday):

Empty DataFrame
Columns: [CAD_EVNT_ID, CREATE_DATE, INCIDENT_DATE, INCIDENT_TIME, NYPD_PCT_CD, BORO_NM, PATRL_BORO_NM, GEO_CD_X, GEO_CD_Y, RADIO_CODE, TYP_DESC, CIP_JOBS, ADD_TS, DISP_TS, ARRIVD_TS, CLOSNG_TS, Latitude, Longitude, WEEK_DAY, INCIDENT_MIN]
Index: []

Let's next filter for early morning times:

df_early_am = filter_by_time(df,times=[0,360])
print(df_early_am[['INCIDENT_DATE','WEEK_DAY','INCIDENT_TIME','INCIDENT_MIN']])

would print:

     INCIDENT_DATE  WEEK_DAY INCIDENT_TIME  INCIDENT_MIN
7       07/04/2021         6      00:01:51      1.850000
27      07/04/2021         6      00:06:12      6.200000
51      07/04/2021         6      00:12:12     12.200000
53      07/04/2021         6      00:12:38     12.633333
54      07/04/2021         6      00:12:38     12.633333
...            ...       ...           ...           ...
1041    07/04/2021         6      05:08:49    308.816667
1068    07/04/2021         6      05:21:49    321.816667
1075    07/04/2021         6      05:24:21    324.350000
1079    07/04/2021         6      05:28:13    328.216667
1111    07/04/2021         6      05:41:34    341.566667

[76 rows x 4 columns]

We can use other methods for clustering, printing out the labels for the July 4 dataset:

print(compute_gmm(df))
print(compute_agglom(df))  

[1 7 1 0 0 1 1 0 0 4 0 2 1 5 5 2 2 1 1 4 4 4 4 5 1 6 3 5 3 3 7 0 7 1 3 3 3
3 1 2 2 7 6 1 1 1 2 0 0 4 5 3 4 6 6 3 1 3 3 1 6 4 6 0 6 6 3 2 6 3 1 1 1 1
4 4 5 2 1 2 2 7 7 1 1 5 3 1 0 5 5 4 4 2 0 0 0 0 2 2 4 4 3 1 1 7 4 3 3 6 6
2 1 0 3 3 1 5 5 2 3 3 1 1 5 5 2 2 0 2 2 3 2 2 1 5 5 1 5 0 0 0 2 2 1 1 5 2
1 3 0 5 5 5 1 1 2 0 0 7 7 7 6 6 3 3 4 4 1 1 1 1 1 3 1 7 4 4 0 1 5 1 3 7 0
4 4 3 1 3 3 0 0 0 0 1 1 1 6 6 0 0 0 0 5 2 2 5 5 3 4 4 1 4 2 0 2 0 2 2 1 1
1 3 3 1 3 3 1 0 0 5 5 1 5 5 1 7 5 2 1 0 0 0 1 5 2 0 2 1 4 4 1 1 4 7 7 3 3
4 1 1 7 7 5 5 0 1 5 1 1 0 7 0 0 2 0 7 7 5 1 2 3 1 1 1 1 3 6 6 4 5 5 2 2 0
3 0 0 2 5 5 0 1 3 7 7 5 5 3 0 6 0 0 1 2 4 5 2 1 3 3 1 1 2 0 1 2 2 2 3 3 4
4 5 5 1 2 0 3 4 3 3 0 1 6 1 1 4 1 4 4 3 6 6 6 2 2 2 3 6 3 3 1 0 5 3 5 2 2
3 3 6 6 2 2 3 6 6 2 0 0 3 3 2 0 3 2 2 3 3 4 4 6 6 1 6 4 5 5 5 4 6 1 1 1 4
2 0 3 5 2 1 3 1 4 3 1 0 3 5 5 5 3 3 7 3 1 2 2 2 4 4 2 2 2 1 1 3 3 2 3 5 1
1 1 0 0 0 0 4 4 5 6 6 6 1 2 2]
[0 6 0 3 3 0 0 3 3 2 3 4 0 7 7 4 4 0 0 2 2 2 2 7 0 0 1 0 1 1 6 3 1 0 1 1 1
1 0 4 4 4 5 0 0 0 4 3 3 2 3 1 2 0 0 1 0 1 1 0 0 2 0 3 0 0 1 4 0 1 0 0 0 0
2 2 3 4 0 4 4 1 1 1 0 3 1 0 3 7 7 2 2 4 3 3 3 3 4 4 2 2 1 0 0 6 2 1 1 0 0
4 0 4 1 1 0 0 0 4 1 1 0 0 7 7 4 4 3 4 4 1 4 4 0 7 7 0 7 3 3 3 4 4 0 0 7 4
0 1 3 7 0 0 0 0 4 3 3 6 6 4 5 5 1 1 2 2 0 0 0 0 0 1 0 6 2 2 3 0 7 0 1 6 3
2 2 1 0 0 0 3 3 3 3 0 0 0 0 5 3 3 3 3 7 4 4 7 7 1 2 2 0 4 4 3 4 6 4 4 0 0
0 1 1 0 1 1 0 3 3 7 7 0 3 3 0 6 3 4 0 3 3 3 0 7 4 3 4 0 2 4 0 0 2 6 6 1 1
2 0 0 6 6 3 3 3 0 7 5 5 3 6 3 3 4 3 6 6 0 0 4 1 0 0 0 0 1 5 5 2 7 7 4 4 3
1 3 3 4 7 7 3 0 1 6 6 7 7 7 3 0 3 3 0 4 2 7 4 0 1 1 1 1 4 3 0 4 4 4 1 1 2
2 0 0 0 4 3 1 2 1 1 3 0 5 0 0 2 0 2 2 1 5 5 5 4 4 4 1 5 1 1 0 3 7 1 3 4 4
1 1 5 5 4 4 1 0 0 4 3 3 1 1 4 3 1 4 4 1 1 2 2 5 5 0 5 2 7 3 3 2 5 0 0 0 2
4 4 1 7 4 0 1 0 2 1 0 3 1 7 3 3 1 1 6 1 0 4 4 4 2 2 4 4 4 0 0 1 1 4 1 3 0
0 0 3 3 3 3 2 2 3 5 5 5 0 4 4]

Lastly, we can use the function compute_explained_variance to assess the best number of clusters:

k_vals = list(range(1,20))
ev = compute_explained_variance(df,K=k_vals)
sns.lineplot(k_vals,ev)
plt.title('Explained Variance for KMeans for Manhattan, 4 July 2021')
plt.show()

will display:

showing a sharp drop-off to K=5 that quickly flattens, showing that additional clusters, beyond 10, do not significantly improve the average distance to the assigned means. This suggests that a reasonable number of clusters is around 8.