Homework 4 for Computer Science 125

Introduction to Computer Science

Boise State University, Spring 1999

CHANGE: Programs 9 and 10 are due by 9pm, Friday, 26 February 1999.
Programs 11 and 12 are due by 9pm, Friday, 5 March 1999.
See the directions in Homework 1 to electronically submit homework.

Warm-up and Practice Problems

These are not be turned in. They are to help you understand the material, and some will appear on exams.

CCJ: Exercise R4.21, p 171.
CCJ: Exercise R5.4, p 222.
CCJ: Exercise R5.14, p 223.
CCJ: Exercise R5.15, p 224.
Your new employer asks you to write the exact program you wrote for your last employer. Is this ethical? What extra circumstances would make this ethical (or not ethical)? Justify your arguments.
Most agree that copying a term paper off the web is unethical, but that using an idea discussed with a friend is not. Who owns an idea? Where do you draw the line? Support your answer with examples.

Graded Problems

P9. Exercise P4.8, p 174. Submit this as program 9 using the electronic submission. Please call the file (and the class) Program9. Also, include an html file called "Program9.html" which calls your applet. (Due 26 February)

Note: your program should terminate if the user enters a negative radius.

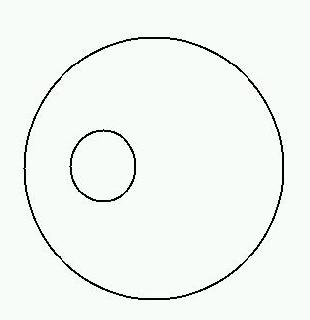
You need to consider the case where one circle is completely contained inside the other, but the circles do not intersect. For example, one such case to consider is:

P10. Exercise P4.10, p 174. Submit this as program 10 using the electronic submission. Please call the file (and the class) Program10. (Due 26 February)

P11. Exercise P5.24, p 231. Submit this as program 11 using the electronic submission. Please call the file (and the class) Program11. (Due 5 March)

Note: This program checks to see if t is a substring of s. Ask the user, first for the string s and then for the string t.

P12. Program 12 will draw a series of triangles that are nested inside of one another. The program starts by the user clicking on three non-collinear points that make the outer triangle. For example:

The program then calls the recursive function descend which takes 3 points as parameters:

public void descend(Point p1, Point p2, Point p3)

The function descend checks if the distance between the first two points is less than 0.5. In which case, it stops. Otherwise, it draws a triangle connecting p1, p2, and p3, calculates the midpoints of the three sides of the triangle, and calls descend again with the midpoints.

The function descend calls two helper functions to calculate the midpoint of a line:

public Point midpoint(Point a, Point b)

and the distance between two points:

public double distance(Point a, Point b)

Submit this as program 12 using the electronic submission. Please call the file (and the class) Program12. Also, include an html file called "Program12.html" which calls your applet. (Due 5 March)