Our goal is to measure how far a turtle will walk over a 500 turns. Here is the basic outline of our program:
1. Set up a turtle, and use it to draw circle boundaries to measure
distance from start.
2. For 500 turns,
3. Choose a random direction: north, west, south, or east
and walk 10 steps in that direction
A sample run of our program looks like this:
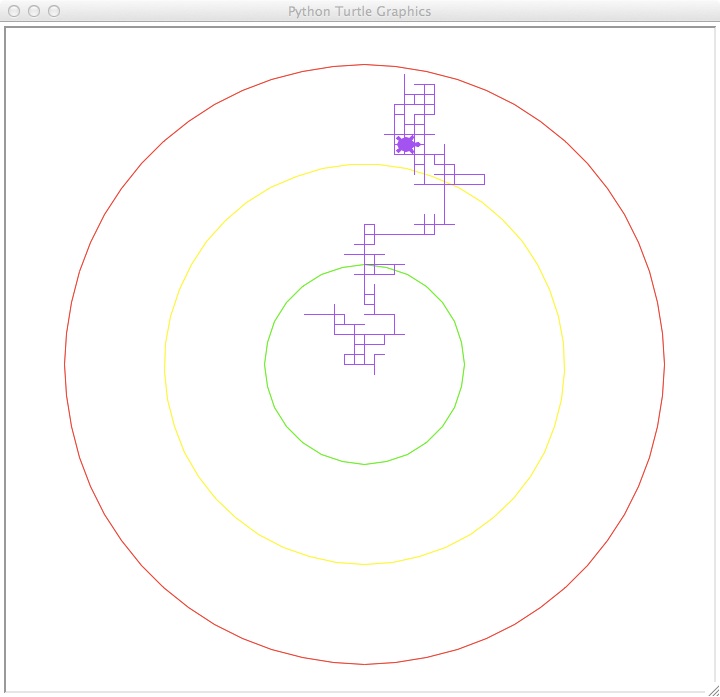
Tess, our turtle, first draws our boundary rings (in green, yellow, and red), then changes to purple to begin her random walk. At each turn, she chooses a random direction and walks 10 steps. This is repeated 500 times.
To choose a random direction, we will use the built-in random number generator from the random library. To use a python library, we include an import statement for that library. So, for this program, we will have two import statements: one for the turtle library and one for the python library:
import turtle import randomThe function random.random() returns a number between 0 and 1. Since we have four different directions, we will divide the possible range into 4 (equal) regions:
- numbers between 0 and 1/4,
- numbers between 1/4 and 1/2,
- numbers between 1/2 and 3/4, and
- numbers between 3/4 and 1.
We can translate all these decisions into python using if and elif constructs:
def main():
tess = setUpTurtle()
for steps in range(500):
direction = random.random()
if direction < 1/4:
tess.right(90)
elif direction < 1/2:
tess.right(180)
elif direction < 3/4:
tess.left(90)
tess.forward(10)
turtle.Screen().exitonclick()
Note that the only way to reach the first elif is if direction was already
bigger than 1/4, so, there is no need to include it in our test statement on the elif.
We hid all the set up in the function, setUpTurtle(), to make the main() function easier to read. In turn, to make setUpTurtle() easier to read, we placed on the repeated statements for creating rings in a function drawRings(). Here is our complete program:
#Walking Turtle program for Intro Programming Lab
import turtle
import random
def drawRing(t,radius,color):
t.up()
t.goto(0,-radius)
t.color(color)
t.down()
t.circle(radius)
def setUpTurtle():
#Create turtle
t = turtle.Turtle()
#Use the turtle to draw the rings:
drawRing(t,100,"green")
drawRing(t,200,"yellow")
drawRing(t,300,"red")
#Return turtle to starting position and set shape, speed, and color:
t.up()
t.home()
t.down()
t.color("purple")
t.shape("turtle")
t.speed(10)
#Return turtle to used elsewhere in the program:
return t
def main():
tess = setUpTurtle()
for steps in range(500):
direction = random.random()
if direction < 1/4:
tess.right(90)
elif direction < 1/2:
tess.right(180)
elif direction < 3/4:
tess.left(90)
tess.forward(10)
turtle.Screen().exitonclick()
main()
Try running it several times. The colored circles indicate 100, 200, and 300 steps from the
starting position. How often does the turtle leave the outer circle? How often does the
turtle finish inside the green circle?