This lab focuses on decisions.

In Lab 3, we started with a program that drew a square to the screen, using turtle graphics: 
import turtle

def main():
    daniel = turtle.Turtle()    #Set up a turtle named "daniel"
    myWin = turtle.Screen()     #The graphics window

    #Draw a square
    for i in range(4):
        daniel.forward(100)     #Move forward 10 steps
        daniel.right(90)        #Turn 90 degrees to the right

    myWin.exitonclick()         #Close the window when clicked
    
main()
Recall, our turtle, named daniel, moved forward 100 steps, made a 90 degree right turn, and then repeated these actions for a total of 4 times. Let's modify it, so, that it will draw an 8 sided polygon: 
import turtle

def main():
	numSides = 8                #Number of sides of the polygon
    daniel = turtle.Turtle()    #Set up a turtle named "daniel"
    myWin = turtle.Screen()     #The graphics window

    #Draw a square
    for i in range(numSides):
        daniel.forward(100)     #Move forward 10 steps
        daniel.right(360/numSides)	#Turn 90 degrees to the right

    myWin.exitonclick()         #Close the window when clicked
    
main()
To make it easier to modify, we stored the number of sides in just one place (the variable named numSides) and use it in range statement in the for-loop as well as calculating the amount needed to turn each time.

Run the program to make sure there's no errors. On the graphics window, you should see an octogon (8-sided) figure. How would you make an octogon like this:

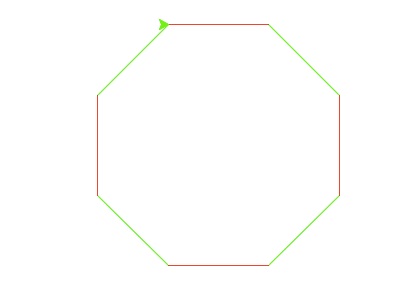
Notice that the edges change colors, the first, third, fifth, and seventh edges are red; while the second, fourth, sixth, and eighth edges are green. Since we start counting with 0, we have that the edges are red when the loop index variable i is 0,2,4,6. The edges are green when the loop index variable is 1,3,5,7.

To make the colors change, we need to test for when the loop index variable is even. A way to say that mathematically is i is even when i divided by 2 has no remainder. In python, we can write that as: 

	if i % 2 == 0:
		daniel.color("red")
Let's add that to our program: 
#Blinking turtle for introductory programming lab

import turtle

def main():
    numSides = 8
    daniel = turtle.Turtle()    #Set up a turtle named "daniel"
    myWin = turtle.Screen()     #The graphics window

    #Draw a square
    for i in range(numSides):
        if i % 2 == 0:
            daniel.color("red")      
        daniel.forward(100)     #Move forward 10 steps
        daniel.right(360/numSides)  #Turn 90 degrees to the right

    myWin.exitonclick()         #Close the window when clicked
    
main()
What does that do? How do we make the color green for when i is odd? Let's add in an else to our if statement: 
	if i % 2 == 0:
		Turn daniel red
	else:
		Turn daniel green
Putting all the pieces together, we get: 
#Blinking turtle for introductory programming lab

import turtle

def main():
    numSides = 8
    daniel = turtle.Turtle()    #Set up a turtle named "daniel"
    myWin = turtle.Screen()     #The graphics window

    #Draw a square
    for i in range(numSides):
        if i % 2 == 0:
            daniel.color("red")
        else:
            daniel.color("green")        
        daniel.forward(100)     #Move forward 10 steps
        daniel.right(360/numSides)  #Turn 90 degrees to the right

    myWin.exitonclick()         #Close the window when clicked
    
main()
Try the program to make sure that the colors change, depending on the value of i. Next, change your program to make a 10-sided polygon (hint: you only need to change one line).