Lab 13
RGGS 670: Algorithmic Approaches to Biological Data
Spring 2016

Topics: Dynamic Programming & Pairwise Alignment of Sequences

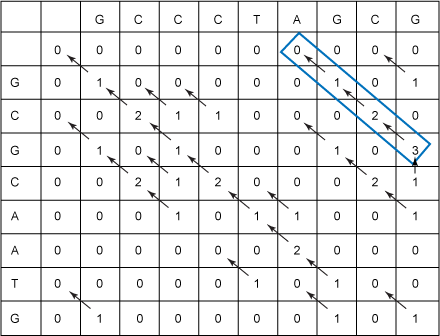
Dynamic Programming

For problems that can be broken into subproblems (and those subproblems occur mulitple times), dynamic programming is often a good approach to compute the answer quickly. The textbook introduces the Manhattan Tourist Problem, which we will implement, and then use the framework developed for it to implement the Needleman-Wunsch algorithm for global pairwise sequence alignment.

Implementing the Manhattan Tourist:

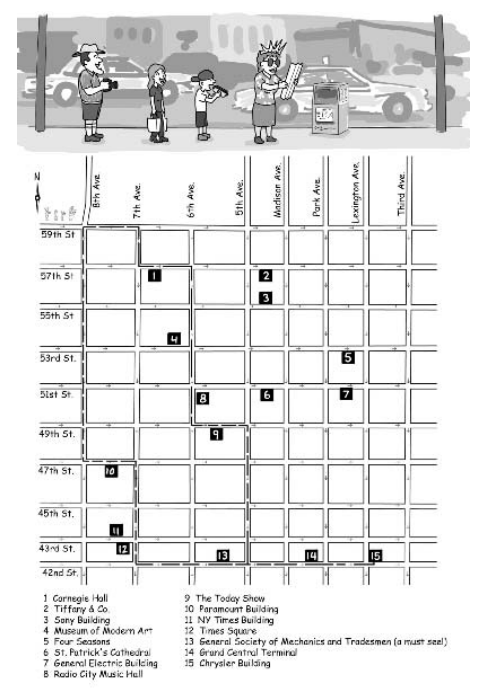
The textbook introduces the Manhattan Tourist problem, where you have a grid of streets with landmarks, and you would like to see as many as possible, without retracing your steps. For example, you start at Columbus Circle (59th Street and 8th Avenue) and finish at 42nd Street and 3rd Avenue:

We can apply this approach to an arbitrarily labeled grid (assume the upper corner has coordinates (0,0) and each increases and the coordinates increase as you progress south and east:

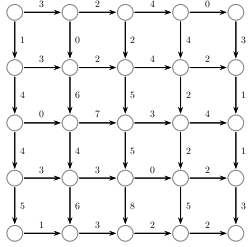
The steps we outlined were:

1. Store best path so far in a grid (array).
2. Fill in the first row and column separately (since there's only one direction from which to reach those cells)
3. Fill in the second row (using the first).
4. Fill in the third row (using the second).
5. Repeat until all rows are filled.
6. The most number of landmarks you can visit is in the bottom right cell.

To do this, we will need:

• south: number of landmarks seen going south from a location.
• east: number of landmarks seen going east from a location.
• best: an array to store the largest possible number of landmarks seen by the time you reach a location.

Let's fill in the steps above (full version, including trace back below is at tourist.py. First, we need to set up the variables:

import numpy as np

#The number of landmarks going east and south from a location:
east = np.array( [[3,2,4,0],[3,2,4,2],[0,7,3,4],[3,3,0,2],[1,3,2,2]] )
south = np.array( [[1,0,2,4,3],[4,6,5,2,1],[4,4,5,2,1],[5,6,8,5,3]] )
size = 5
best = np.zeros( (size,size) )

#Check to make sure this matches figure:
print "east:", east
print "south:", south

Now, let's fill out first row and column of the grid:

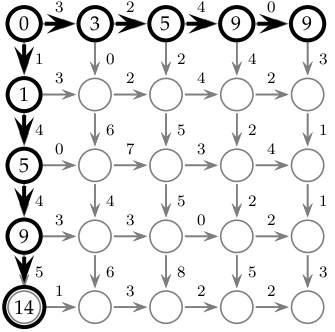
so that the upper corner is 0, and the elements in the first column depend just on the elements above them, and similarly, the elements in the first row depend on those to their left:

best[0,0] = 0
for i in range(1,size):
     best[0,i] = best[0,i-1] + east[0,i-1]
     best[i,0] = best[i-1,0] + south[i-1,0]

#Check that it works:
print best     

To fill in the rest of the array, we use the larger of the total seen entering going east and entering going south:

#Fill in the rest of the array:
for i in range(1,size):
     for j in range(1,size):
          best[i,j] = max(best[i,j-1] + east[i,j-1], best[i-1,j] + south[i-1,j])

#Check that it works:
print best

Once we check that the above works, then we can add in the code that "reads off" the path from computatations. The easiest way to do this is to create a second matrix, traceback that keeps track of the direction from which the best path enters each element. To the top of the file, let's add code that creates a 2D array of dimensions (size,size) to hold the traceback. numpy arrays only take numbers, but when figuring out the path, it is easier to think of words "UP" and "LEFT" (then numbers. To make the code easier to read, we will create variables called UP = 1 and LEFT = -1 and use those:

traceback = np.zeros( (size,size) )
UP = 1
LEFT = -1

Now, when we compute the values for best, let's also keep track of where they came:

#Set up first row and first column to gap:
best[0,0] = 0
for i in range(1,size):
     best[0,i] = best[0,i-1] + east[0,i-1]
     best[i,0] = best[i-1,0] + south[i-1,0]
     traceback[i,0] = UP
     traceback[0,i] = LEFT

print traceback

#Fill in the rest of the array:
for i in range(1,size):
     for j in range(1,size):
          best[i,j] = max(best[i,j-1] + east[i,j-1], best[i-1,j] + south[i-1,j])
          if best[i,j-1] + east[i,j-1] > best[i-1,j] + south[i-1,j]:
               traceback[i,j] = LEFT
          else:
               traceback[i,j] = UP

print traceback

Once we have the traceback, we can use it to create the path. We'll start at the lower left corner (i.e. (i,j) = (size-1,size-1)) and then we write down the value we stored in the traceback for it, go to that point, write down its value, and repeat until we reach the origin:

path = ""
i = size-1
j = size-1
while i > 0 or j > 0:
     if traceback[i,j] == UP:
          path = "south " + path
          i = i - 1
     else:
          path = "east " + path
          j = j -1

print path

Check to make sure that your path is correct before continuing to sequence alignment.

Alignment of Sequences

The same underlying idea works for aligning sequences. Below, we will implement Needleman-Wunsch's algorithm for global alignment of sequences (a complete version of this program is in globalAlign.py.

Global Alignment of Sequences

Let's modify the previous program to implement the Smith-Waterman algorithm. We'll follow the same format as for the Manhattan Tourist problem. First, we will set up variables for:

• our inputs (in this case, the sequences),
• an array to keep track the best way to reach each element,
• an array to keep track of the path (traceback),
• variables to make the code easier to read (e.g. size, UP, LEFT, DIAG)

Here's the first code that does this:

import numpy as np

#Some test sequences:
seq1 = "TATATAGG"
seq2 = "TAGAG"

size1 = len(seq1)+1
size2 = len(seq2)+1
best = np.zeros( (size1,size2) )
traceback = np.zeros( (size1,size2) )

UP = 1
LEFT = -1
DIAG = 2

For alignment, we need to specify the gap penalty (delta) and the scoring function, (sigma(x,y)):

delta = 1

def sigma(x,y):
     if x == y:
          return 1
     else:
          return -1

Now that we have the preliminaries set up, let's fill in the first row and column of the matrices:

#Set up first row and first column to gap:
best[0,0] = 0
for i in range(1,size1):
     best[i,0] = best[i-1,0] - delta
     traceback[i,0] = UP

for i in range(1,size2):
     best[0,i] = best[0,i-1] - delta
     traceback[0,i] = LEFT

print best
print traceback

Before continuing, print out the matrices to make sure they are correct.

Now, as above, we use a nested loop to fill in the remaining entries. In addition to LEFT and UP from the Manhattan Tourist Problem, we also are allowed to travel diagonally (DIAG) which gives one more clause to the definitions:

#Fill in the rest of the array:
for i in range(1,size1):
     for j in range(1,size2):
          best[i,j] = max(best[i,j-1] - delta, \
                          best[i-1,j] - delta, \
                          best[i-1,j-1] + sigma(seq1[i-1],seq2[j-1]))
          if best[i-1,j-1] + sigma(seq1[i-1],seq2[j-1]) == best[i,j]:
               traceback[i,j] = DIAG
          elif best[i-1,j] - delta == best[i,j]:
               traceback[i,j] = UP
          else:
               traceback[i,j] = LEFT
print "best: ", best
print "traceback: ", traceback

Again, before continuing, print out the matrices to make sure they are correct.

Once we have found the path, we need to read off the alignment. As in the above case, we start in the lower right hand corner and work our way back to (0,0):

path1 = ""
path2 = ""
i = size1-1
j = size2-1
while i > 0 or j > 0:
     if traceback[i,j] == UP:
          path1 = seq1[i-1] + path1
          path2 = "-" + path2
          i = i - 1
     elif traceback[i,j] == LEFT:
          path1 = "-" + path1
          path2 = seq2[j-1] + path2
          j = j -1
     else:
          path1 = seq1[i-1] + path1
          path2 = seq2[j-1] + path2
          i -= 1
          j -= 1

print "An alignment is:"
print path1
print path2

Experiment with different sequences to verify that the alignment works.

Local Alignment of Sequences

(Image from Paul Reiners, IBM, 2008)

The Smith-Waterman Algorithm for local alignment is very similar to our local alignment code. It has the following changes:

• The first row and column are initialized to 0.
• At each element, we take the maximum value of 4 things:
  • best[i,j-1] - delta,
  • best[i-1,j] - delta,
  • best[i-1,j-1] + sigma(seq1[i-1],seq2[j-1]), and
  • 0
• To find the best local alignment, find the largest value in the matrix and traceback from it until an element has value 0.

Challenge

• Modify your global alignment program to follow the Smith-Waterman algorithm described above.
• Optional: print out the top 3 local alignments from the matrix.

Lab Report

For each lab, you should submit a lab report by the target date to: kstjohn AT amnh DOT org. The reports should be about a page for the first labs and contain the following:

Target Date: 4 May 2016
Title: Lab 13: Sequence Alignment
Name & Email:

Purpose: Give summary of what was done in this lab.
Procedure: Describe step-by-step what you did (include programs or program outlines).
Results: If applicable, show all data collected. Including screen shots is fine (can capture via the Grab program).
Discussion: Give a short explanation and intepretation of your results here.

Using Rosalind

This course will use the on-line Rosalind system for submitting programs electronically. The password for the course has been sent to your email. Before leaving lab today, complete the first two challenges.