Adjacency Matrices
Can you get here from there? Say you an airlines that flies:
- New York to/from Chicago
- New York to/from Houston
- Chicago to/from San Francisco
- Houston to/from San Fransisco
Can you fly from New York to San Francisco? Well, not directly, but it is possible if you change plans in Chicago or Houston. We can represent this in a matrix with entries of 1 if there is a flight and 0 if there is not:
| New York | Chicago | Houston | San Jose |
| New York | 1 | 1 | 1 | 0 |
| Chicago | 1 | 1 | 0 | 1 |
| Houston | 1 | 0 | 1 | 1 |
| San Jose | 0 | 1 | 1 | 1 |
We're making the assumption that if you start in a city, you can stay in the city (i.e. there is a `self-loop' from New York to New York). You can also model this without self-loops, depending on the application.
Let's use a dictionary so, we don't have to remember which index corresponds to which city:
cityNum = {}
cityNum["New York"] = 0
cityNum["Chicago"] = 1
cityNum["Houston"] = 2
cityNum["San Jose"] = 3
Using numpy, the matrix (without labels):
import numpy as np
flights = np.zeros( (4,4) )
flights[cityNum["NYC"],cityNum["Chicago"]] = 1
flights[cityNum["NYC"],cityNum["Houston"]] = 1
flights[cityNum["Chicago"],cityNum["NYC"]] = 1
flights[cityNum["Chicago"],cityNum["NYC"]] = 1
flights[cityNum["Houston"],cityNum["NYC"]] = 1
flights[cityNum["Houston"],cityNum["San Jose"]] = 1
flights[cityNum["San Jose"],cityNum["Chicago"]] = 1
flights[cityNum["San Jose"],cityNum["Houston"]] = 1
#Create the self-loops:
for i in range(4): flights[i,i] = 1
(complete program in
flights.py).
We can reach San Francisco from New York by taking flights to an intermediary city (in this case, Chicago or Houston) and then continuing on. That is:
There are flights: (NYC -> Chicago and Chicago -> San Jose) or (NYC -> Houston and Houston -> San Jose)
In the matrix, we have existing flights as 1 and no flight as 0, so instead of the
and, we can multiply and just check that sum is greater than 0 (the sum is non-zero only when one of the terms is, which happens exactly when there's flights via the intermediary cities):
(NYC -> Chicago * Chicago -> San Jose) + (NYC -> Houston * Houston -> San Jose) > 0
In terms of math, we are taking a vector of the outgoing flights from a city and combining it with a vector of the incoming flights to the next city. This combination is called the dot product:
v dot w = v1*w1 + v2*w2 + ... vN*wN
where the vectors are v = (v1, v2, ... vN) and w = (w1, w2,... wN).
In numpy, there is a built-in function for taking the dot product of matrices (often called `multiplying matrices', though the numpy matrix multiplication does something very different).
This is a lovely feature of using adjacency matrices to reprensent graphs. If there is an edge from a to b and an edge from b to c, then a to c is non-zero in the matrix A.dot(A). Why? The i,jth element of the A.dot(A) is the dot product of the row indexed by i by the column index by j, which is:
A[i,0]*A[0,j] + A[i,1]*A[1,j] + A[i,2]*A[2,j] + ... + A[i,n-1]*A[n-1,j]
This entry is not zero, only when one of the terms of the sum is not zero (there's no cancelling since all distances are positive).
The result of A.dot(A) is:
| New York | Chicago | Houston | San Francisco |
| New York | 3 | 2 | 2 | 2 |
| Chicago | 2 | 3 | 2 | 2 |
| Houston | 2 | 2 | 3 | 2 |
| San Francisco | 2 | 2 | 2 | 3 |
That is, we can get from every city to every other city (the values indicate the number of different ways to do so, including taking the 'self-loops' or empty flights).
Before continuing, let's draw the cities we have. To do, we'll use basemap focused on the US (complete program in
flights.py). In github, there is already a dictionary set up with entries for cities and there longitude and latitudes
major_us_city_dma_codes.
Instead of typing the coordinates in by hand, we will access the dictionary entries for each city we're mapping.
- Set up a dictionary with city names and coordinates from file.
- Set up a basemap with state boundaries.
- Include our flight table as a numpy array.
- Draw a marker on each city in the flights table.
- For each edge in the table, draw a great circle between the cities.
- TO DO: Compute the cities that can be reached in two flights.
- TO DO: Draw the cities and great circles for those flights.
Try the program and see how it works.
Challenges
- Add three additional cities to the flights table. Not all cities appear in the major_us_city_dma_codes file, so, make sure to choose cities that do. Add in extra flights between the cities (only modifying the flights and cityNum data structures) and display.
- Change your program so it displays all cities that can be reached in 3 or fewer flights (i.e. use flights.dot(flights).dot(flights) instead of flights for your edges between cities).
- You have frequent flier miles that allow you to fly on many, but not all flights on a certain airlines. Can you fly from New York to Portland using only flights from the listed in cityPairs.txt? Use your program from above to answer the question.
Hint: If you find entering all the city-pairs by hand into the flights table tedious, assign numbers to each city (either by reading in the file and using those or setting by hand), then read in the file line-by-line and set flights[c1,c2] = 1 if c1 and c2 occur together on the line.
Adjacency Lists
A good use of adjacency lists is for storing sparsely populated graphs, such as trees. In this part of the lab, we will write a function that prints out all the leaves in a clade of a tree.
It is not hard, but a bit tedious, to parse a tree in Newick format (since you need to worry about extra spaces, names of more than one character, etc.). The file adjTrees.py has a tree already stored as an adjacency list in the dictionary tree. Pictorally, the tree is:
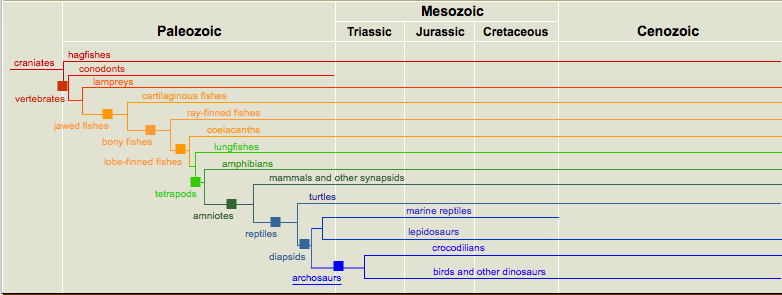
(Image from Smithsonian Institute)
The entries in our dictionary have the following structure:
(parentName,[child1,child2,...])
If there are no children, the last part of the tuple is an empty list.
The goal of this part of the lab is to write a function that given a vertex name, v, to print out all leaves below it. Let's break this into parts:
printLeaves(v):
If v is a leaf, print out v
Else, for each child of v, printLeaves(child)
Let's translate that into Python:
def printLeaves(v):
if len(adjList[v][1]) == 0:
print v
else:
for child in adjList[v][1]:
printLeaves(child)
Try running the program adjTrees.py.
Challenges
- Using the program as a template, write a function that returns the number of leaves beneath a vertex.
- Using the program as a template, write a function that returns the height of vertex (i.e. how many levels of the tree are above it, or the length of the path to the leave farthest away).
Hint: First think about what level a leave is at, and then what level a parent is, given the height of its children.
