Lab 1
RGGS 670: Algorithmic Approaches to Biological Data
Spring 2016

Today's lab begins with a quick tutorial on using Python, the built-in turtle and random libraries, and the on-line bioinformatics challenges, Rosalind. The main focus is on simulating Brownian motion by 1D and 2D random walks.
Software tools needed: Python IDLE programming environment and a web browser (for accessing lab and Rosalind).

Using Python

We will be using the IDLE programming environment for Python. The Python programming language and IDLE environment are freely available for many platforms from python.org. For this class, we are using Python 2, which is part of the Mac OSX operating system. Many features of the language (including the syntax of print statements) changed between the second and third version, and many popular packages are still only available for the second version.

To launch IDLE on your Macintosh:

1. Open the Applications folder.
2. Inside it, open the Utilities folder.
3. Launch the Terminal application.
4. The terminal will open a window where you can type commands. In that window, type:

   idle

   (remember to hit the enter/return key, so, the computer realizes you're done typing).
5. Another window should open. Test to see if it is working by typing:

   print "Hello!"

   (remember to hit the enter/return key, so, the computer realizes you're done typing).

Once you have IDLE running, you can keep it in your dock by clicking on it and choosing options.

Turtle Library & for loops

For our first programs, we will use a built-in library (file of useful commands) for drawing using turtles. We will begin with a simple program and modify it to add functionality. This can be done from the Python prompt ( >>> in IDLE), but it is easier to store the program in a file and modify the file. To do this, go to the File menu of IDLE and choose New File (or type ⌘N).

In the new file window, type:

    import turtle

    teddy = turtle.Turtle()
    for i in range(4):
        teddy.forward(100)
        teddy.right(90)
    
    turtle.exitonclick()

Indentation does matter, so, remember to indent the lines after the for, using TABs, so that they are included in the for-loop. Save the file as firstProgram.py.

Notes on saving files:

• You can save your programs as almost anything, except the names of libraries (e.g. turtle or random). Using a library name will confuse Python-- it will think your program should be used instead of the similarly named library.
• Saving your program with the .py extension is not necessary, but it is good form. Also, any file with a .py extension will be displayed nicely (color coding of keywords, etc.)

To run your program, go to the Run menu and choose Run Module. Python should open a new graphics window and draw a square.

Line-by-Line

What is this program doing? Let's go through, line-by-line:

• The first line

      import turtle

  tells Python that you would like to use some of the commands contained in the module, called, turtle.
• The next line creates a turtle object that can be used in the program:

      teddy = turtle.Turtle()

  I named my turtle after President Roosevelt, but you can use any name you would like (as long as you spell it the same throughout).
• A for statement is used to repeatedly perform sequences of statements (so called a ``loop''). This for-loop repeats actions 4 times:

      for i in range(4):

  To repeat the actions more times, you can change the parameter to the range statement. For example, range(6) in our loop would repeat the actions 6 times.
• Inside our for-loop, we have our turtle perform 2 actions: walk forward 100 steps, and then turn 90 degrees:

          teddy.forward(100)
          teddy.right(90)

• The last command keeps the graphics window open until the mouse is clicked. When clicked, the window will close and the program will end.

      turtle.exitonclick()

Some Challenges

Modify your program to:

1. Draw a hexagon.
2. Draw an octagon.
3. What does the following do? Work through it on paper, and then implement in Python to verify:

       import turtle
   
       teddy = turtle.Turtle()
       for i in range(40):
           teddy.forward(10*i)
           teddy.right(90)
       
       turtle.exitonclick()
   

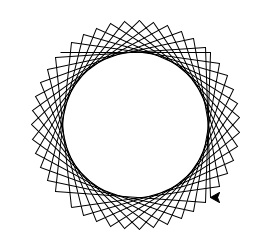
4. Implement the following piece of pseudocode (i.e. directions that look very similar to code) as a complete program using turtle graphics:

       Repeat 45 times:
           Walk forward 100 steps
           Turn right 92 degrees
       

   Your output should look similar to:
   

5. Draw a 5-pointed star.
6. Print your name to the Python prompt 50 times.

Random Library

Another useful library is random library that generates (pseudo)-random numbers. The following:

	import random           #use the random library
		
	# other code here....
		
	random.randrange(7)

generates a random whole number between 0 and 6. Similarly, the command

	random.randrange(360)

generates a random whole number between 0 and 359. The command also allows random numbers to be chosen from multiples. For example:

• random.randrange(0,100,2) chooses a random even number that's greater than 0 and less than 100.
• random.randrange(0,360,90) chooses a random number from the sequence 0, 90, 180, 270.

Let's write a program that turns a random amount each time. Here is an outline in comments (anything after the `#' is ignored by Python):

#Include the random and turtle libraries
#Create a turtle
#Have a loop that repeats 25 times
	#Inside that loop, 
	#Move forward 10 steps
	#Turn a random amount
#Close window on mouse click

Try to fill in each piece (if you're stuck, here is a possible solution).

Some Challenges

Modify your program to:

1. Modify your random turning program to make random turns of 90 degrees only (i.e. 0, 90, 180, 270 degrees only).
2. Modify your random turning program to make random turns of 180 degrees only (i.e. 0 and 180 degrees only).

Simulating Brownian Motion with Random Walks

We can use the programs above to simulate `random walks' where an object moves in a random direction (and a random distance forward). Random walks are well studied for modeling Brownian motion, diffusion models, paths of foraging animals, fluctuations in stock prices, and genetic drift.

For this lab, we will use the random turn programs to gather data to affirm or refute the hypothesis:

The longer the walk, on average, the farther east or west from the origin it ends.

Some notes:

• Test this hypothesis for all three types of random turns: 1 degree, 90 degrees, and 180 degree turns.
• The turtle library has several commands for reporting position. A useful one here is xcor() which gives the x coordinate of the turtle.
• For each length = 100, 200, 300, 400, 500, simulate 10 runs and report the average of the x position for each length walk.

Lab Write-Up

For each lab, you should submit a lab report by the target date to: kstjohn AT amnh DOT org. The reports should be about a page for the first labs and contain the following:

Target Date: 1 February 2016
Title: Lab 1: Simulating Brownian Motion with Random Walks
Name & Email:

Purpose: Give summary of what was done in this lab.
Procedure: Describe step-by-step what you did (include programs or program outlines).
Results: Show all data collected. Including screen shots is fine (can capture via the Grab program).
Discussion: Give a short explanation and interpretation of your results here.

Using Rosalind

This course will use the on-line Rosalind system for submitting programs electronically. The password for the course has been sent to your email. Before leaving lab today, complete the first challenge.