CSci 39542 Syllabus    Resources    Coursework


Program 7: Housing Model
CSci 39542: Introduction to Data Science
Department of Computer Science
Hunter College, City University of New York
Spring 2022

Classwork    Quizzes    Homework    Project   

Program Description


Program 7: Housing Model.   Due noon, Thursday, 17 March.
Learning Objective: to enhance on statistical skills and understanding via computation linear regression and loss functions.
Available Libraries: pandas, numpy and core Python 3.6+.
Data Sources: NYC Department of City Planning (DCP) Housing Database and Neighorhood Tabulation Areas.
Sample Datasets: Housing_Database_by_NTA.csv, NYC_population_by_NTA.csv.

This program continues the analysis from Program 6 of the NYC Housing Database.

NYC Department of City Planning (DCP) Housing Database contains all approved construction and demolition jobs since 2010. Summary information about it are provided via OpenData NYC. A summary, recorded as net housing units, by Neighborhood Tabulation Areas:

The DCP also provides a summary of population in New York City from the 2000 and 2010 censuses, organized by neighborhood tabulation areas (NTAs):

In Program 6, we looked at which features are most correlated with the increase in housing units. For this program, we will explore linear models for the dataset, as well as the data separated by borough:

The assignment is broken into the following functions to allow for unit testing:

For example, if the housing and population data files are downloaded (and your functions are imported from a file answer), then a sample run of the program: 

df = p7.make_df('Housing_Database_by_NTA.csv', 'New_York_City_Population_By_Neighborhood_Tabulation_Areas.csv')
print('The DataFrame:')
print(df.head())
And the first lines would be: 
The DataFrame:
   OBJECTID       boro  ...                        NTA Name Population
1       195  Manhattan  ...  Stuyvesant Town-Cooper Village      21049
3       166      Bronx  ...                  West Concourse      39282
5        37      Bronx  ...                       Bronxdale      35538
7        14   Brooklyn  ...                         Midwood      52835
9        65  Manhattan  ...                       Yorkville      77942

[5 rows x 32 columns]
We can use our next function to compute a regression line for the Population and total columns: 
theta_0, theta_1 = p7.compute_lin_reg(df['Population'],df['total'])
print(f'The regression line has slope {m} and y-intercept {b}.')
which prints: 
The slope is 0.4536370834220062 and the y-intercept is -625.3358497794688.
We can check if our function that computes this directly is returning the same values as the sklearn package: 
from sklearn import linear_model
reg = linear_model.LinearRegression()
X = pd.DataFrame(df['Population'])
y = pd.DataFrame(df['total'])
reg.fit(X,y)
print(f'For sklearn, the slope is {reg.coef_[0][0]} with y-intercept: {reg.intercept_[0]}.')
which prints: 
For sklearn, the slope is 0.45363708342200604 with y-intercept: -625.3358497794616.
We can plot the original data with the regression line: 
import matplotlib.pyplot as plt
xes = np.array([0,df['Population'].max()])
yes = theta_1*xes + theta_0
plt.scatter(df['Population'],df['total'])
plt.plot(xes,yes,color='r')
plt.title(f'Regression line with m = {theta_1:{4}.{2}} and y-intercept = {theta_0:{4}.{4}}')
plt.show()
would give the plot:

Next, let's test out the function that computes by borough. We note that for the default value of boro = ['All'], the function will be identical to compute_lin_reg: 

theta_0, theta_1 = p7.compute_boro_lr(df,'Population','total')
print(f'The slope is {theta_1} and the y-intercept is {theta_0}.')
which prints, as expected: 
The slope is 0.4536370834220062 and the y-intercept is -625.3358497794688.
For other values of boro, it will restrict the data set to those boroughs: 
si_0, si_1 = p7.compute_boro_lr(df,'Population','total',boro=['Staten Island'])
print(f'SI:  The slope is {si_1} and the y-intercept is {si_0}.')
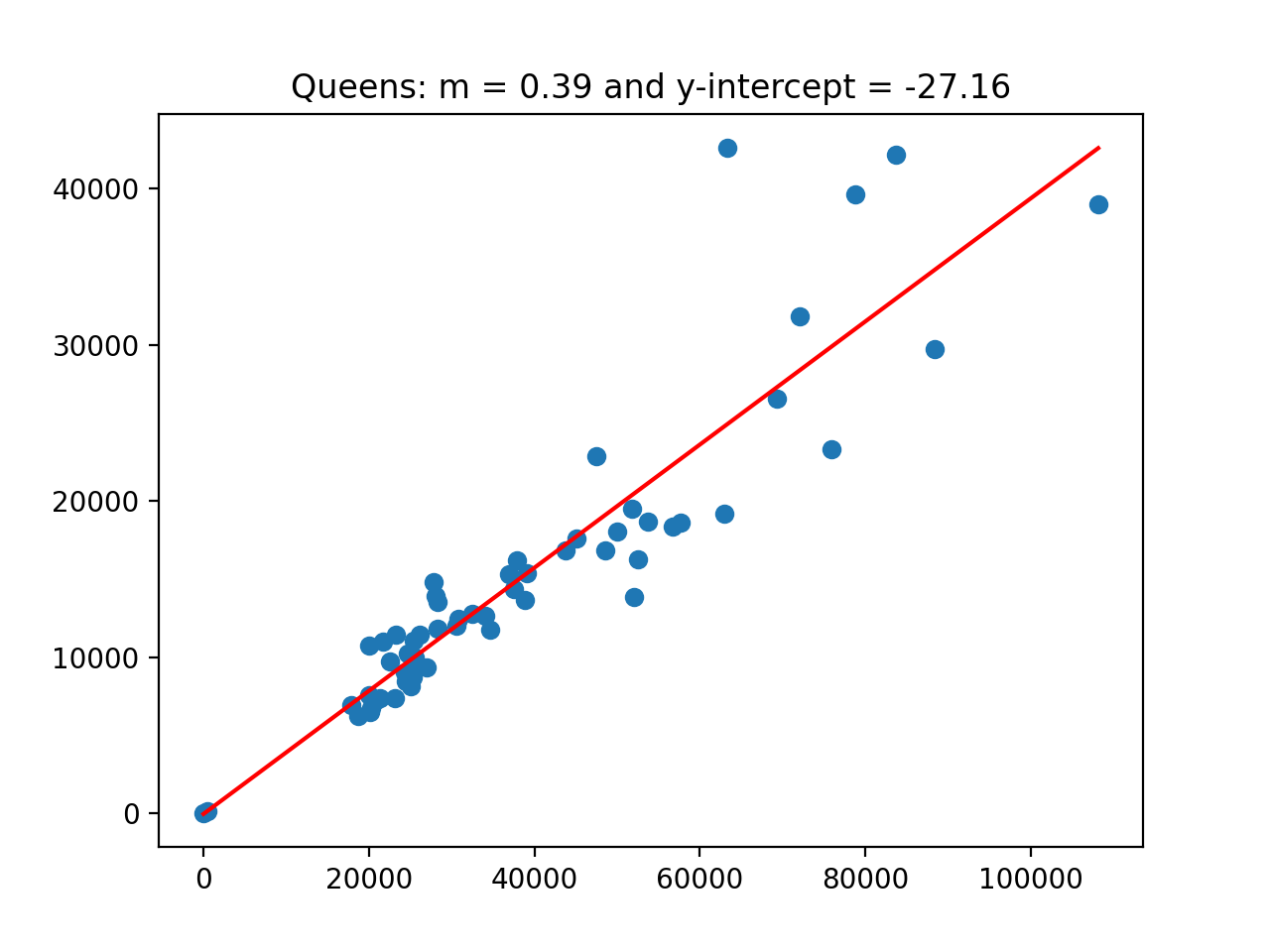
q_0, q_1 = p7.compute_boro_lr(df,'Population','total',boro=['Queens'])
print(f'Queens: The slope is {q_1} and the y-intercept is {q_0}.')
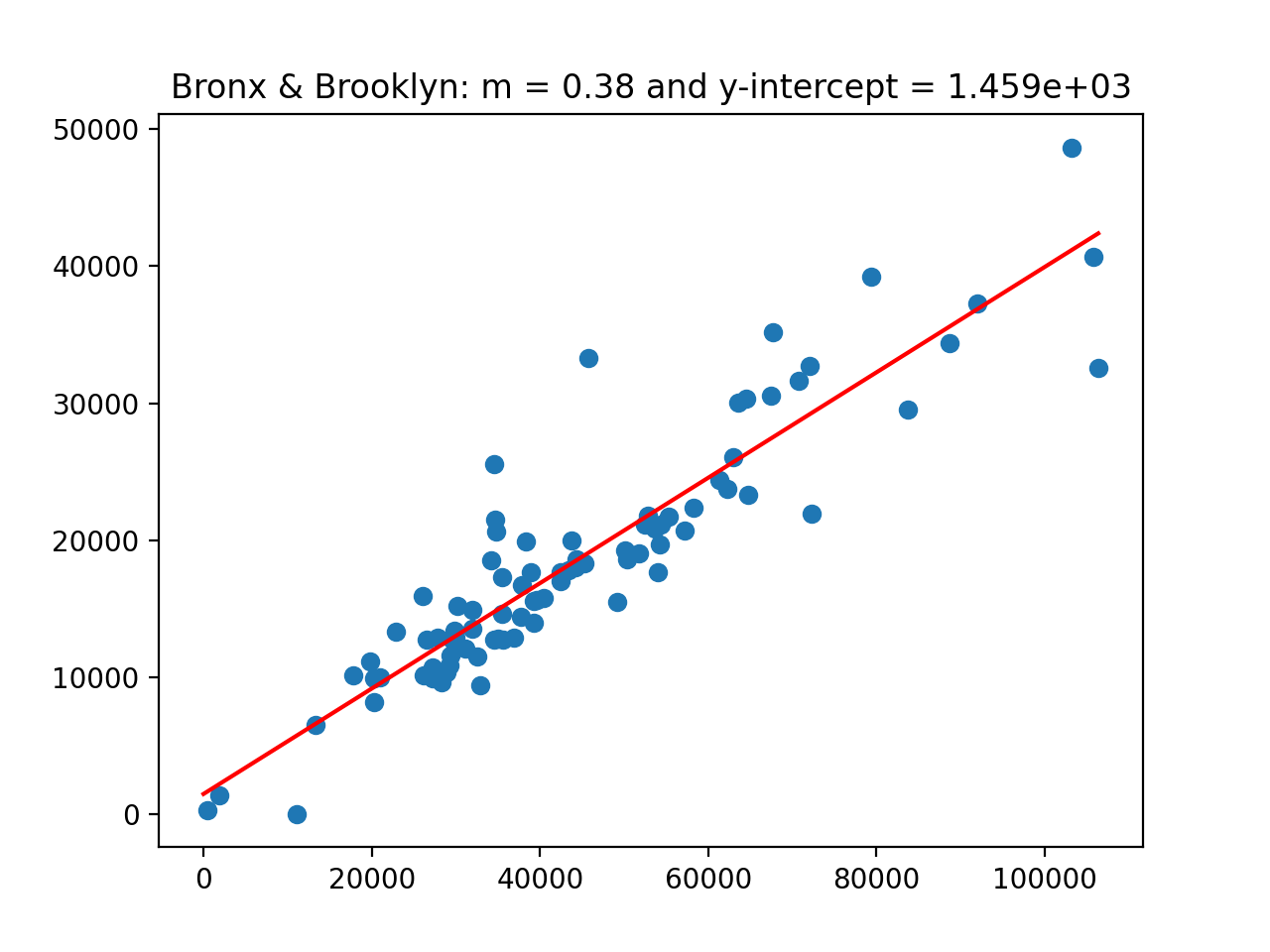
b_0, b_1 = p7.compute_boro_lr(df,'Population','total',boro=['Bronx','Brooklyn'])
print(f'B&B: The slope is {b_1} and the y-intercept is {b_0}.')
which prints: 
SI:  The slope is 0.3892292629712051 and the y-intercept is -2.5490753943668096.
Queens: The slope is 0.39404151495697937 and the y-intercept is -27.156488411430473.
B&B: The slope is 0.3849458413516747 and the y-intercept is 1458.8043454328654.
(Images corresponding to the various values of boro = ['All'] are above.)

Lastly, we have functions that will compute the error using different loss functions. Let's start with identical columns, to make sure the functions return 0: 

loss = p7.compute_error(df['total'],df['total'])
print(f'The loss is {loss} for total vs total.')
which prints: 
The loss is 0.0 for total vs total.
Now, trying the function on our models: 
y_est = theta_0 + theta_1*df['Population']
loss = p7.compute_error(df['total'],y_est)
print(f'The loss is {loss} for default loss function: MSE.')
loss = p7.compute_error(df['total'],y_est,loss_fnc= p7.RMSE)
print(f'The loss is {loss} for RMSE.')
which prints: 
The loss is 28443412.98831634 for default loss function: MSE.
The loss is 5333.23663344468 for RMSE.